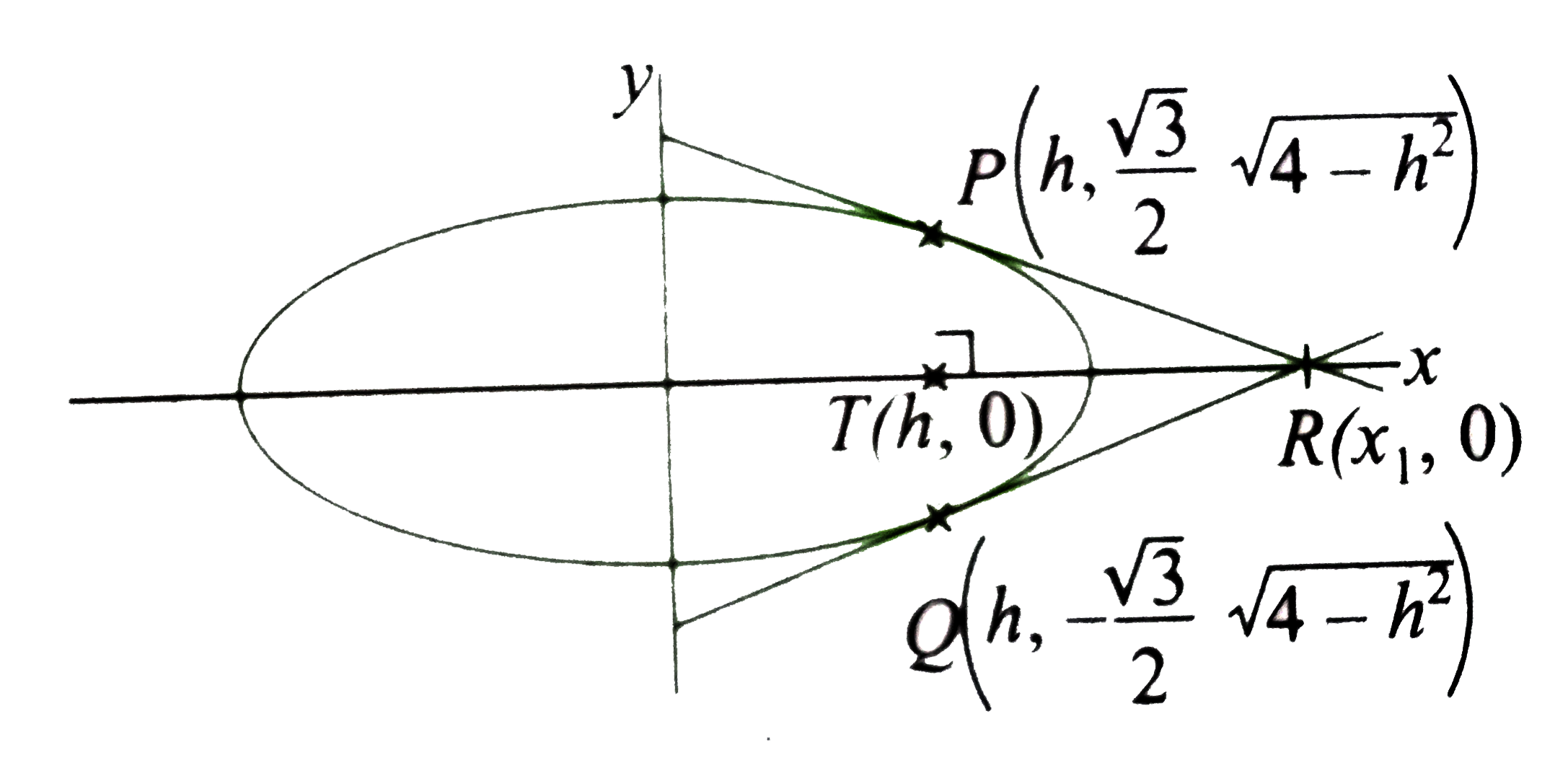
A vertical line passing through the point (h,k) intersects the ellipse $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ at points P and Q. Let the tangents to the ellipse at Pa dn Q meet at point R. If $Δ (h)$ = area of triangle $P Q R, Δ_{1} = max 1 / 2 \leq h \leq 1 Δ h, and Δ_{2} = min 1 / 2 \leq h \leq 1 Δ (h), then \frac{8}{\sqrt{5}} Δ_{1} - 8 Δ_{2} =$ __________

Video Solution

Text Solution

Verified by Experts

$\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$
$∴ Y = \frac{\sqrt{3}}{2} \sqrt{4 - h^{2}} at x = h$
Let $R (x_{1}, 0)$
PQ, is the chord of contant So, $\frac{x x_{1}}{4} = 1$
or $x = \frac{4}{x_{1}}$
Which is the euation of PQ. At x=h
$\frac{x}{x_{1}} = h or x_{1} = \frac{4}{h}$
$Δ (h) = Area of Δ P Q R = \frac{1}{2} \times P Q \times R T$
$= \frac{1}{2} \times \frac{2 \sqrt{3}}{2} \sqrt{4 - h^{2}} \times (x_{1} - h) = \frac{\sqrt{3}}{2 h} {(4 - h^{2})}^{3 / 2}$
Clearly, $Δ h = \frac{45 \sqrt{5}}{8} at h = \frac{1}{2}$
and $Δ_{2}$ Minimum of $Δ (h) = \frac{9}{2} a t h = 1$
So, $\frac{8}{\sqrt{5}} Δ_{1} - 8 Δ_{2} = \frac{8}{\sqrt{5}} \times \frac{45 \sqrt{5}}{8} - \times \frac{9}{2} = 45 - 36 = 9$

Updated on:21/07/2023

the tangent and normal to the tangent to the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ at the point $(3, \frac{- 9}{2})$ , then the area ( in sq units ) of the $Δ P Q R$ Is
A $\frac{16}{3}$
B $\frac{14}{3}$
C $\frac{34}{15}$
D $\frac{68}{15}$
Any tangent at a point $P (x, y)$ to the ellipse $\frac{x^{2}}{8} + (y^{2}) = 1$ meets the coordinate axes in the points A and B such that the area of the triangle OAB is least, then the point P is
A $(\sqrt{8}, 0)$
B $(0, \sqrt{18})$
C $(2, 3)$
Dnone
The muinimum area of the triangle formed by the tangent to $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ and the coordinate axes is
Aab
B $\frac{a^{2} + b^{2}}{2}$
C $\frac{{(a + b)}^{2}}{2}$
D $\frac{a^{2} + a b + b^{2}}{3}$