Tangents are drawn from the point P(3, 4) to the ellipse x29+y24=1 touching the ellipse at points A and B.
(3,0)and(0,2)
(−8/5,2√161/15)and(−9/5,8/5)
(8/5,2√161/15and(0,2)
(3,0)and(−9/5,8/5)
Given ellipse x29+y24=1
The equation of tangent having slope m is 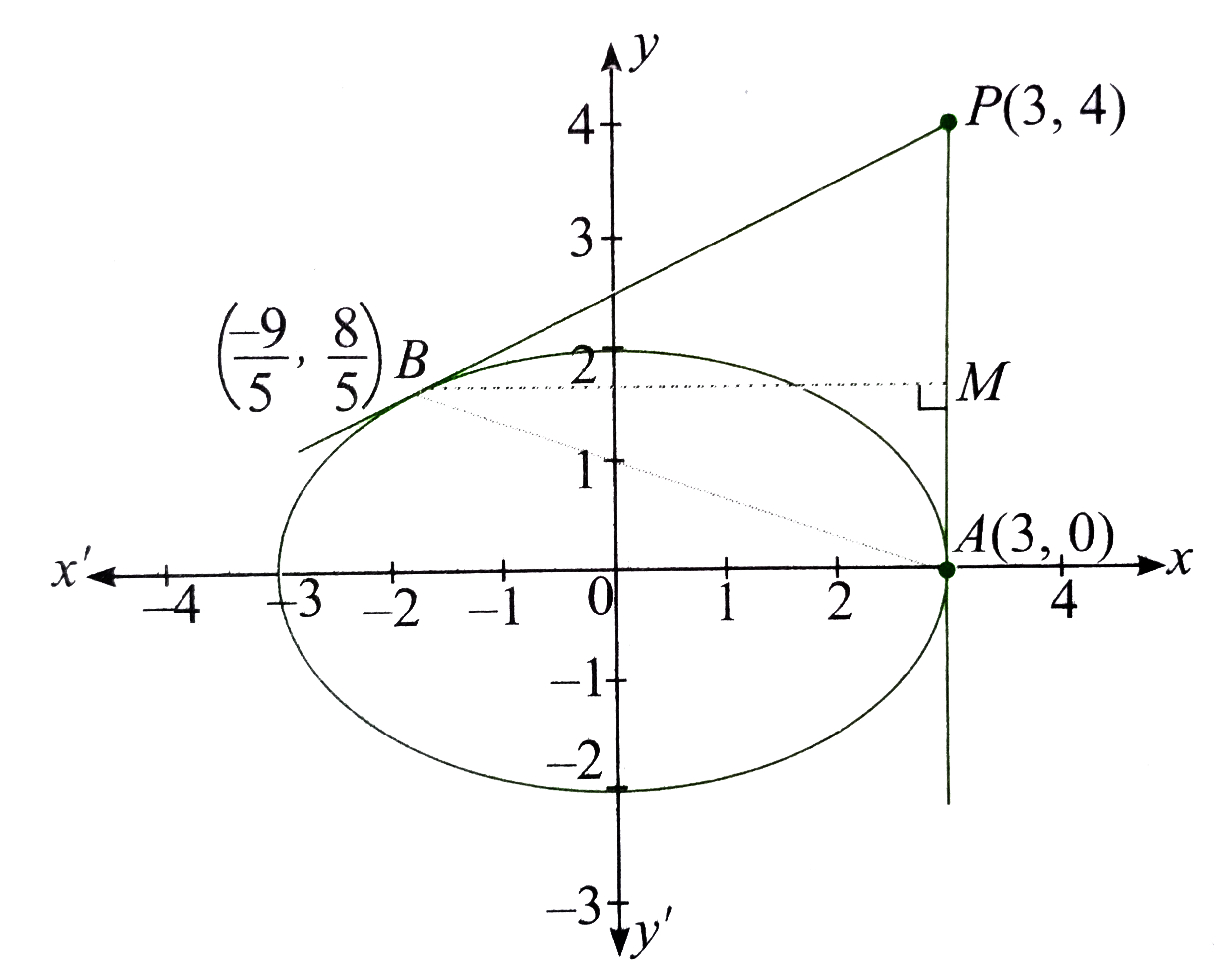
y=mx+√9m2+4
Sqaring , we have
16+9m2−24m=9m2+4
or m=1224=12
Threrefpre, the equation of tangent is y−4=−(x−3)prx−2y+5=0 (1)
Let the point of contact on the curve be B(α,β)
Equation of tangent at this point is xα9+yβ4−1=0 (2)
Comparing equations (1) and (2)
α/91=β/4−2=−15
or α=−95,β=85 ∴B≡(−95,85)
Another slope of tangent is ∞ then the equation of tanents is x=3 and the coresponding point of cocntact is A(3,0)
Similar Questions
Tangents are drawn from a point P(6,√5) to the ellipse x225+y216=1touching the ellipse in the points Q and R. The angle between PQ and PR is
View SolutionTangent are drawn from the point (3, 2) to the ellipse x2+4y2=9 . Find the equation to their chord of contact and the middle point of this chord of contact.
View Solution
Knowledge Check
Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The coordinates of A and B are
A(3,0) amd (0,2)B(−85,(2√16115)and(−98,85)C(−85,(2√16115)and(0,2)D(3,0)and(−95,85)Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The orthocenter of the trianlge PAB is
A(5,87)B(75,258)C(115,85)D(825,75)Tangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at points A and B.
The equation of the locus of the point whose distance from the point P and the line AB are equal, is:A(9x2+y2−6xy−54x−62y+241=0Bx2+9y2+6xy−54x+62y−241=0C9x2+9y2−6xy−54x−62y−241=0Dx2+y2−2xy+27x+31y−120=0
Tangents are drawn from the point P(3,4) to the ellipsex29+y24=1 touching the ellipse at the point A and B then the equation of the locus of the point whose distance from the point P and the line AB are equal, is
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at point A and B. Q. The coordinates of A and B are
View SolutionTangents are drawn from the point P(3, 4) to the ellipse x29+y24=1 touching the ellipse at points A and B. The orthocenter of the triangle PAB is
View SolutionTangents are drawn from the point P(3,4) to the ellipse x29+y24=1 touching the ellipse at points A and B.
The equation of the locus of the point whose distance from the point P and the line AB are equal, is:
View SolutionAngle between the tangents drawn from point (4, 5) to the ellipse x216+y225=1 is
View Solution