Question

Consider
two straight lines, each of which is tangent to both the circle $x^2+y^2=\frac{1}{2}$
and the
parabola $y^2=4x$
. Let these
lines intersect at the point $Q$
. Consider
the ellipse whose center is at the origin $O(0,0)$
and whose
semi-major axis is $OQ$
. If the
length of the minor axis of this ellipse is $\sqrt{2}$
, then
which of the following statement(s) is (are) TRUE?

Options

A. For the ellipse, the eccentricity is `(1)/(sqrt(2))` and the length the latcus rectue is 1
B. For the ellipse, the eccentricity is `(1)/(2)` and the length the latcus rectue is `(1)/(2)`
C. The erea of the reagion bounded by the ellipse between the lines `x=(1)/(sqrt(2)) and x=1 "is" (1)/(4sqrt(4)) (pi-2)`
D. The erea of the region bounded by the ellipse between the lines `x=(1)/(sqrt(2)) and x=1 "is" (1)/(16)(pi-12)`

Explanation

Equation of tangent of parabola `y^(2)=4x` having slop is `y=mx+(1)/(m)` ltbr If this is tangent to circle `x^(2)+y^(2)=1//2`.
If this is tangent of circle `x^(2)+y^(2)=1//2`, then distance form centre of the circle from the line is equal to radius.
`:.|(0+0+(1)/(m))/(sqrt(1+m^(2)))|=(1)/(sqrt(2))`
`:. m^(4)+m^(2)-2=0`
`:. m=+-`
Euqation of common tangens are `y=x+1 and y=-x-1`
These tangents intersects at point Q which is (-1,0) .
`:. OQ=1`
Let the equation of ellipese be `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
`:. a=OQ=1`
Let the equation of ellipse be `(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`
`:.a=OQ=1`
also, given that `2b=sqrt(2) or b=(1)/(sqrt(2))`
Thererfore, equation of ellipse is `(x^(2))/(1)+(y^(2))/(1//2)=1`
`e=sqrt(1-(b^(2))/(a^(2)))=sqrt(1-(1)/(2))=(1)/(sqrt(2))`
`L.R.=(2b^(2))/(a)=1`

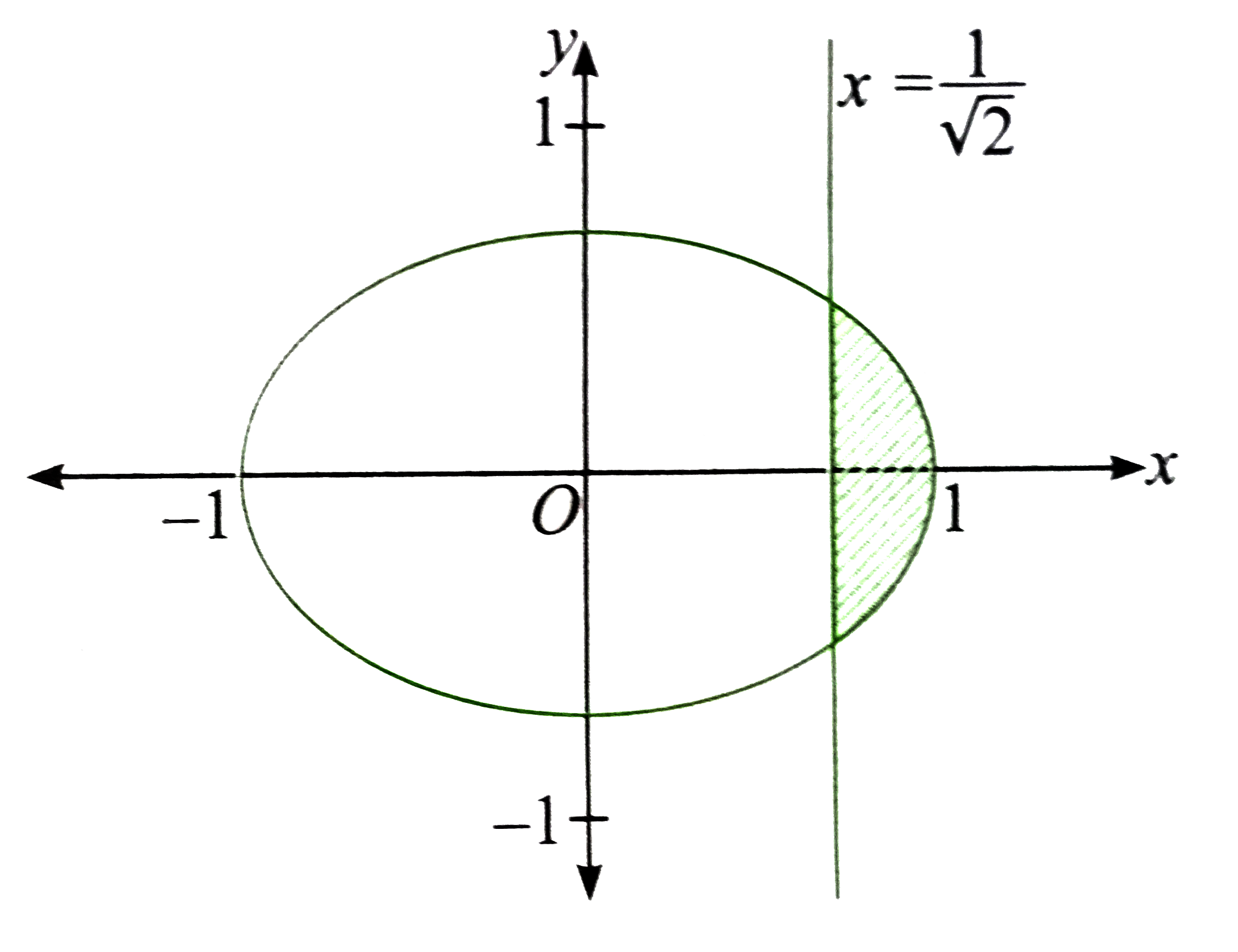
Leh the area bounded by ellipse and lines `x=(1)/(sqrt(2)) and x=1` be A.
`A=2xxunderset(1//sqrt(2))overset(1)int(1)/(sqrt(2))sqrt(1-x^(2))dx`
`=sqrt(2)[(x)/(2)sqrt(1-x^(2))+(1)/(2)sin^(-1)x]_(1//sqrt(2))^(1)`
`=sqrt(2)[(pi)/(4)-((1)/(4)+(pi)/(8))]=sqrt(2)((pi)/(8)-(1)/(4))=(pi-2)/(4sqrt(2))`