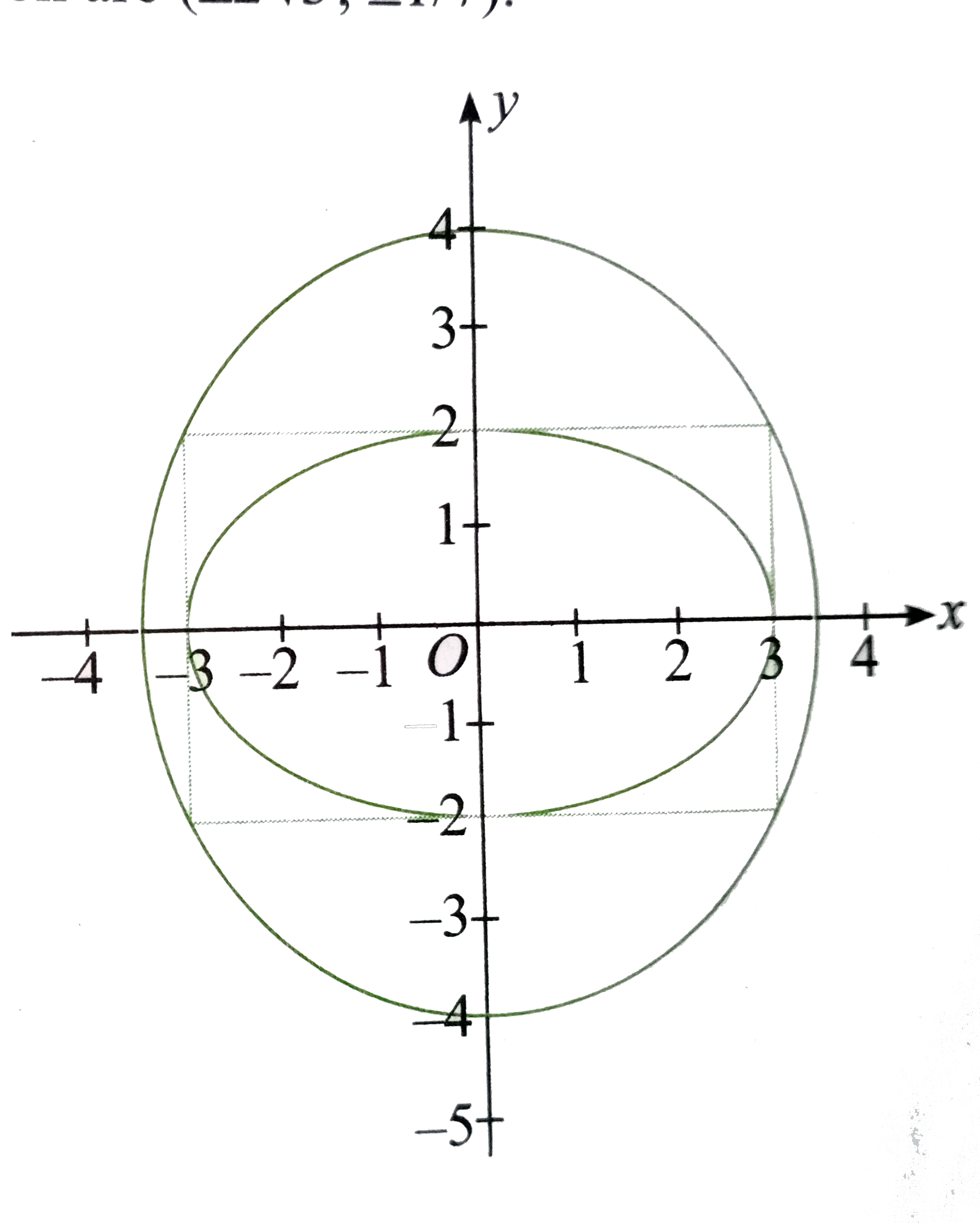
The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
√2/2
√3/2
1/2
3/4
Let the ellipse be
x2a2+y2b2=1
as it passing through (0,4) and (3,2). So,
b2=16and9a2+(4)+(16)=1
or a2=12 ltbr So, 12=16(1−e2)
or e=12
Similar Questions
The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinates axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The length (in units) of the major axis of ellipse E2 is
View Solution
Knowledge Check
- Question 1 - Select One
The ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) x2+16y2=16 (2) x2+12y2=16 (3) 4x2+48y2=48 (4) 4x2+64y2=48
Ax2+12y2=16B4x2+48y2=48C4x2+64y2=48Dx2+16y=16 - Question 2 - Select One
The ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) x2+16y2=16 (2) x2+12y2=16 (3) 4x2+48y2=48 (4) 4x2+64y2=48
Ax2+16y2=16Bx2+12y2=16C4x2+48y2=16D4x2+64y2=48 - Question 3 - Select One
If F1(-3, 4) and F2 (2, 5) are the foci of an ellipse passing through the origin, then the eccentricity of the ellipse is
A√295+√29B√215+√29C√265+√29D√295+√21
If the ellipse x2a2+y2b2=1 is inscribed in a rectangle whose length to breadth ratio is 2 :1 then the area of the rectangle is
View SolutionThe ellipse E:x225+y216=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. A hyperbola (with same centre and transverse axis same as major axis of ellipse) intersects the ellipse orthogonally and passes through the vertices of the rectangle.Then eccentricity of the hyperbola is
View SolutionThe eccentricity of the ellipse 5x2+9y2=1 is a.2/3 b. 3/4 c. 4/5 d. 1/2
View SolutionAn ellipse has foci (4, 2), (2, 2) and it passes through the point P (2, 4). The eccentricity of the ellipse is
View SolutionThe eccentricity of the ellipse, which passes through the points (2, −2) and (−3,1) is :
View Solution

