The normal at a point $P$ on the ellipse $x^{2} + 4 y^{2} = 16$ meets the x-axis at $Q \dot{}$ If $M$ is the midpoint of the line segment $P Q,$ then the locus of $M$ intersects the latus rectums of the given ellipse at points. $(\pm \frac{(3 \sqrt{5})}{2} \pm \frac{2}{7})$ (b) $(\pm \frac{(3 \sqrt{5})}{2} \pm \frac{\sqrt{19}}{7})$ $(\pm 2 \sqrt{3}, \pm \frac{1}{7})$ (d) $(\pm 2 \sqrt{3} \pm \frac{4 \sqrt{3}}{7})$

$(\pm 3 \sqrt{5} / 2, \pm 2 / 7)$

$(\pm 3 \sqrt{5} / 2, \pm \sqrt{19} / 7)$

$\pm 2 \sqrt{3}, \pm 17)$

$(\pm 2 \sqrt{3}, \pm 4 \sqrt{3} / 7)$

Video Solution

Text Solution

Verified by Experts

Given ellipse is $\frac{x^{2}}{16} + \frac{y^{2}}{4} = 1$ . Normal at $P (4 \cos ϕ, 2 \sin ϕ)$ ,
given by $4 x \sec ϕ - 2 y cosec ϕ = 12$
It meets x-axist at
Let $M \equiv (α, β)$
be the point of PQ.

$∴ α = \frac{3 \cos ϕ + 4 \cos ϕ}{2}$
$= \frac{7}{2} \cos ϕ$
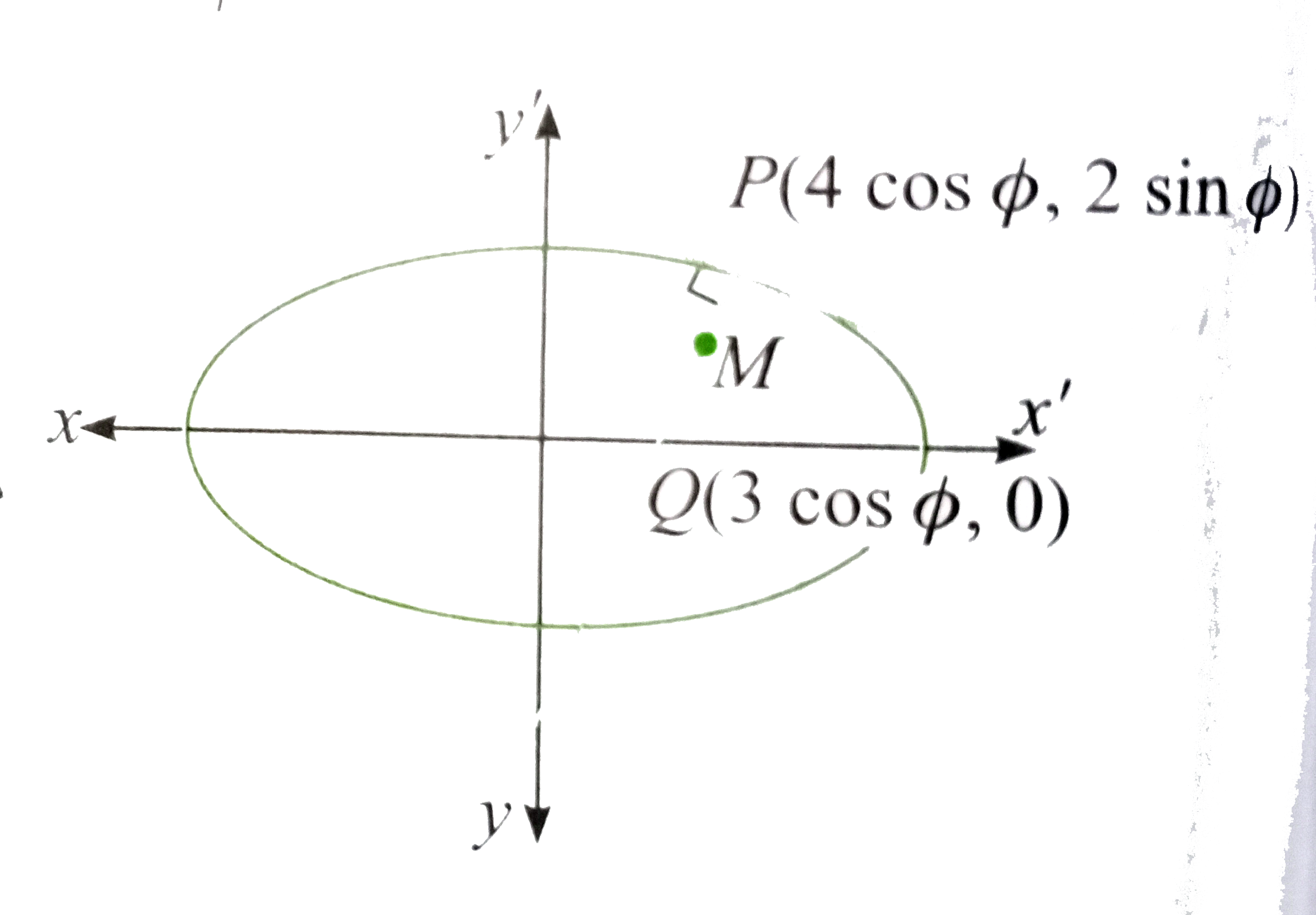
or $\cos ϕ = \frac{2}{7} α$
Using $\cos^{2} ϕ + \sin^{2} ϕ = 1$ , we have
$\frac{4}{49} α^{2} + β^{2} = 1$
or $\frac{4}{49} x^{2} + y^{2} = 1$
Now, the rectum lines of given ellipse are $x = \pm 2 \sqrt{3}$
Solving (1) and (2), we have
$\frac{48}{49} + y^{2} = 1$
$or y = \pm \frac{1}{7}$
The points of intersection are $(\pm 2 \sqrt{3}, \pm 1 / 7)$

Updated on:21/07/2023

The normal at a point $P$ on the ellipse $x^{2} + 4 y^{2} = 16$ meets the x-axis at $Q .$ If $M$ is the midpoint of the line segment $P Q,$ then the locus of $M$ intersects the latus rectums of the given ellipse at points. $⎛ ⎜ ⎜ ⎝ \pm \frac{(3 \sqrt{5})}{2} \pm \frac{2}{7} ⎞ ⎟ ⎟ ⎠$ (b) $⎛ ⎜ ⎜ ⎝ \pm \frac{(3 \sqrt{5})}{2} \pm \frac{\sqrt{19}}{7} ⎞ ⎟ ⎟ ⎠$ $(\pm 2 \sqrt{3}, \pm \frac{1}{7})$ (d) $(\pm 2 \sqrt{3} \pm \frac{4 \sqrt{3}}{7})$
A $(\pm \frac{3 \sqrt{5}}{2}, \pm \frac{2}{7})$
B $(\pm \frac{3 \sqrt{5}}{2}, \pm \frac{\sqrt{19}}{7})$
C $(\pm 2 \sqrt{3}, \pm \frac{1}{7})$
D $(\pm 2 \sqrt{3}, \pm \frac{4 \sqrt{3}}{7})$