The ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is
x2+16y2=16
x2+12y2=16
4x2+48y2=16
4x2+64y2=48
The correct Answer is:B
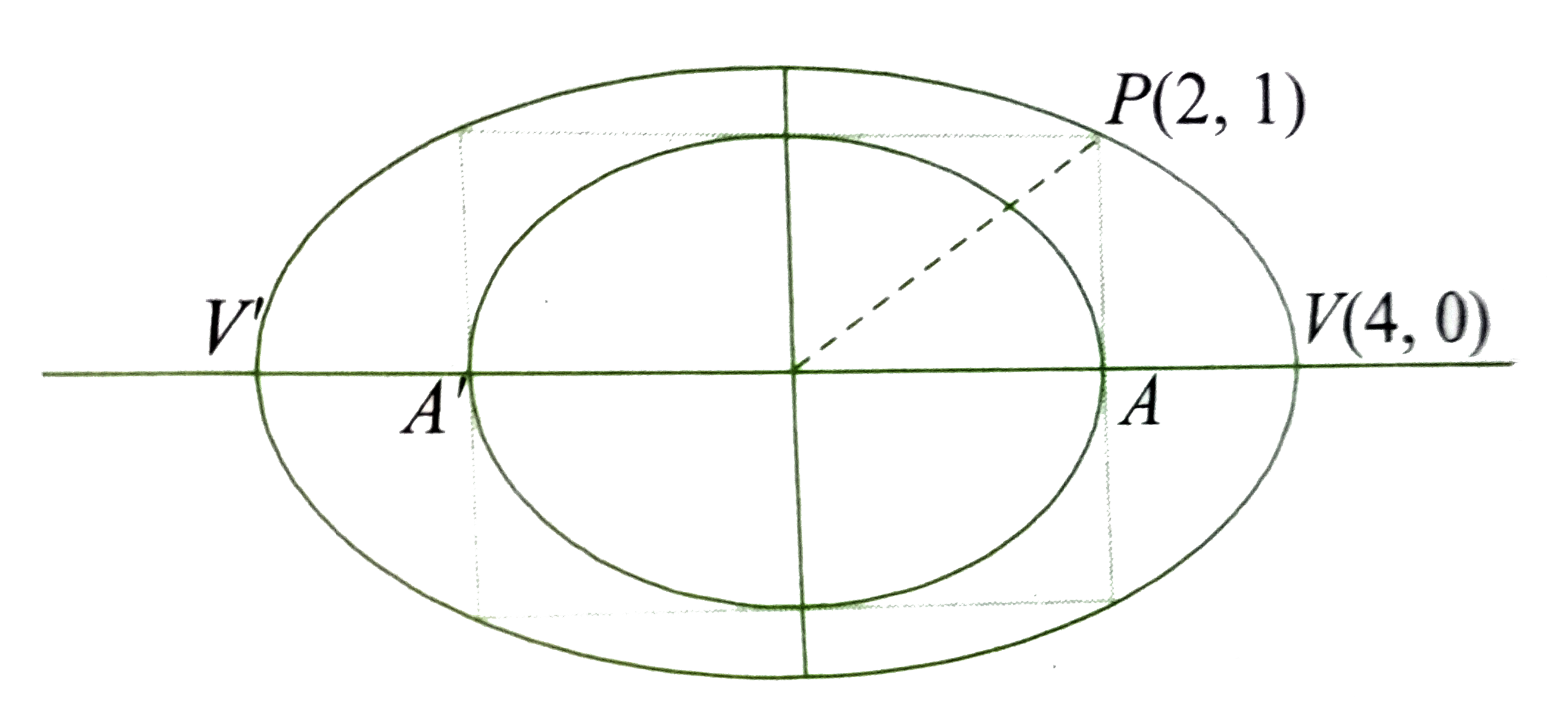
x2+4y2=4⇒x24+y21=1
So, a=2,b=1
Thus P is (2,1)
The required ellipse is x2a2+y2b2=1⇒x242+y2b2=1
The point (2,1) lis on it.So
416+1b2=1⇒1b2=1−14=34⇒b2=43
∴x216+y2(43)=1⇒x216+3y24=1⇒+12y2=16
Similar Questions
Major axis on the x-axis and passes through the points (4,3) and (6,2). find equation of ellipse.
View SolutionThe ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinates axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The length (in units) of the major axis of ellipse E2 is
View Solution
Knowledge Check
The ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) x2+16y2=16 (2) x2+12y2=16 (3) 4x2+48y2=48 (4) 4x2+64y2=48
Ax2+16y2=16Bx2+12y2=16C4x2+48y2=16D4x2+64y2=48Ellipse x2+4y2=4 is inscribed in a rectangle aligned with co-ordinate axes . This rectangle itself is inscribed in another ellipse the passes ellipse that through (-4,0) . Then the equation of the ellipse is
Ax2+16y2=16Bx2+12y2=16C4x2+48y2=48D4x2+64y2=48The equation of the ellipse passes through the points (4,0) and (0,2) is
Ax24+y216=1Bx216+y24=1Cx24+y22=1Dx22+y24=1
The ellipse E1:x29+y24=1 is inscribed in a rectangle R whose sides are parallel to the coordinate axes. Another ellipse E2 passing through the point (0, 4) circumscribes the rectangle R. The eccentricity of the ellipse E2 is √22 (b) √32 (c) 12 (d) 34
View Solutionif vertices of an ellipse are (−4,1),(6,1) and x−2y=2 is focal chord then the equation of the ellipse is
View SolutionAn ellipse has foci (4, 2), (2, 2) and it passes through the point P (2, 4). The eccentricity of the ellipse is
View SolutionIf F1(-3, 4) and F2 (2, 5) are the foci of an ellipse passing through the origin, then the eccentricity of the ellipse is
View SolutionAn ellipse with focii (0,±2) has length of minor axis as 4 units. Then the ellipse will pass through the point
View Solution
