Consider the ellipse whose major and minor axes are x-axis and y-axis, respectively. If ϕ is the angle between the CP and the normal at point P on the ellipse, and the greatest value tanϕ is 34 (where C is the centre of the ellipse). Also semi-major axis is 10 units . The eccentricity of the ellipse is
A
50 units
B
100 units
C
25 units
D
none of these
Video Solution
Text Solution
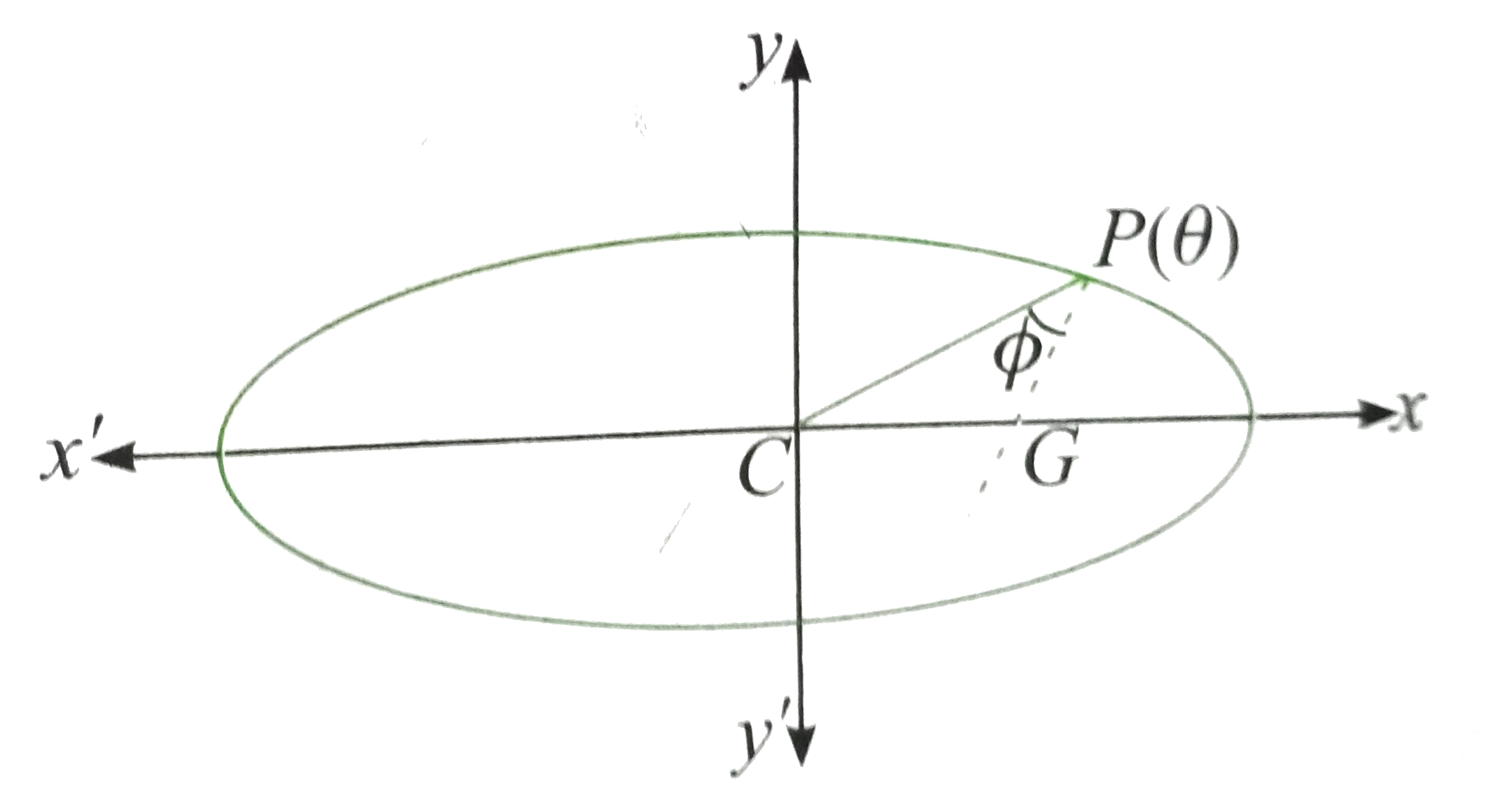
Let P be any point on the ellipse t (acosθ,bsinθ)
Therefore, the equation of CP is
y=(batanθ)x
The normal to the ellipse at P is
axcosθ−bxsinθ=a2−b2
Slopes of the lines CPand the normal GP are (b/a) tanθ and (a/b) tan,θ respectively. Therefore,
tanϕ=abtanθ−batanθ1+abtanθbatanθ
a2−b2ab=tanθsec2θ
=a2−b2absinθcosθ=a2−b22absin2θ
Therefore , the greatest value of tanϕ is
x2−b22ab×1=a2−b22ab
Given that
a2−b22ab=32
Let ab=t
∴t−1t=32
or 2t2−3t−2=0
or2t2−4t+t−2=0
or(2t+1)(t−2)
ab=2
or e2=1−14
or e=√32
The rectangle inscribed in the ellipse, whose one vertexis a(cosθ,bsinθ),is(2acosθbsinθ)=2absin(2θ) which has maximum, value 2ab. Given that a=10. Then b=5. Therefore, the maximum area is 100
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
Let x+6y=8 is tangent to standard ellipse where minor axis is 4√3, then eccentricity of ellipse is
A√56B√1112C(13)√113D(14)√1112 - Question 2 - Select One
If the normal at any point P on the ellipse cuts the major and minor axes in G and g respectively and C be the centre of the ellipse, then
Aa2(CG)2+b2(Cg)2=(a2−b2)2Ba2(CG)2−b2(Cg)2=(a2−b2)2Ca2(CG)2−b2(Cg)2=(a2+b2)2DNone of these - Question 3 - Select One
If the angle between the lines joining the end points of minor axis of an ellipse with its foci is π2 then the eccentricity of the ellipse is
A1/2B1/√2C√3/√2D1/2√2
The order of the differential equation of ellipse whose major and minor axes are along x-axis and y-axis respectively, is
View SolutionThe equation of an ellipse, whose major axis = 8 and eccentricity = 1/2, is
View SolutionThe length of the latus rectum of an ellipse is 13 of the major axis. Its eccentricity is
View SolutionIf the length of the major axis of an ellipse is 178 times the length of the minor axis, then the eccentricity of the ellipse is
View SolutionIf the angle betweent he lines joining the end points of minor axis of an ellipse with its foci is π2, then the eccentricity of the ellipse is
View Solution

