The locus of the image of the focus of the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{9} - 1, (a > b),$ with respect to any of the tangents to the ellipse is ${(x + 4)}^{2} + y^{2} = 100$ (b) ${(x + 2)}^{2} + y^{2} = 50$ ${(x - 4)}^{2} + y^{2} = 100$ (d) ${(x + 2)}^{2} + y^{2} = 50$

${(x + 4)}^{2} + y^{2} = 100$

${(x + 2)}^{2} + y^{2} = 50$

${(x - 4)}^{2} + y^{2} = 100$

${(x - 2)}^{2} + y^{2} = 50$

Video Solution

Text Solution

Verified by Experts

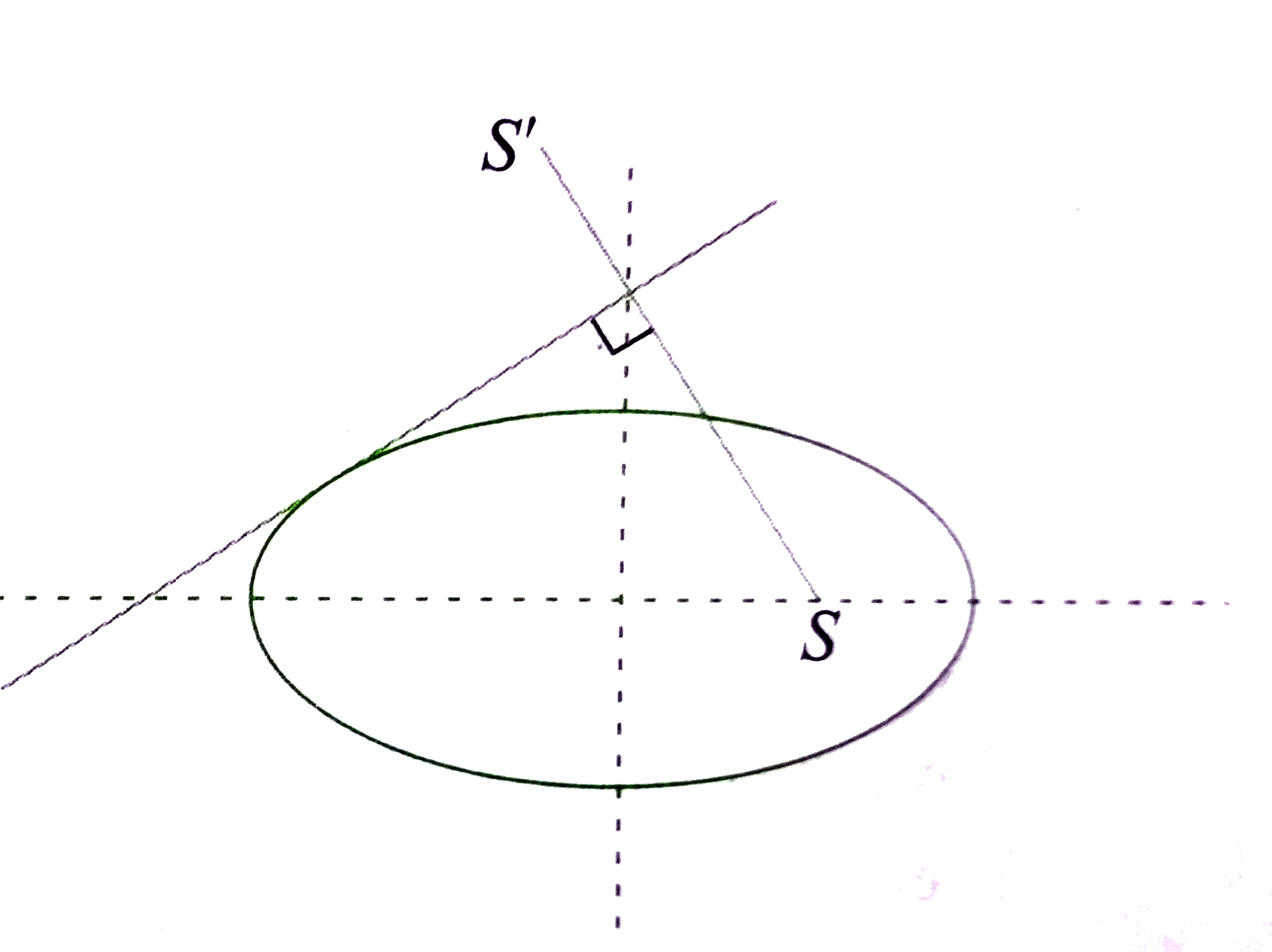
Let S''(h,k)be the image.
SS'' cuts a tangents at a point which lies on the auxiliary circle of the ellipse. Therefore,
$(\frac{h \pm 4}{2}) + \frac{k^{2}}{4} = 25$
Hence the locus is $(x \pm 4) + y^{2} = 100$

Updated on:21/07/2023

The locus pf the image of the focus of the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ , with the respect to any of the tangent to the ellipse is
A ${(x + 4)}^{2} + y^{2} = 100$
B(x+2)^(2)+y^(2)=50
C ${(x - 4)}^{2} + y^{2} = 100$
D $(x - 20^{2} + y^{2} = 50$
The coordinates of a focus of the ellipse $4 x^{2} + 9 y^{2} = 1$ are
A $(\frac{\sqrt{5}}{6}, 0)$
B $(- \frac{\sqrt{5}}{6}, 0)$
C $(\frac{\sqrt{3}}{6}, 0)$
D $(- \frac{\sqrt{3}}{6}, 0)$
The locus of pole of tangents to the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ with respect to the parabola $y^{2} = 4 a x,$ is
A $b^{2} y^{2} = a^{2} (x^{2} - a^{2})$
B $b^{2} y^{2} = 4 a^{2} (x^{2} + a^{2})$
C $b^{2} y^{2} = 4 a^{2} (x^{2} - a^{2})$
D $b^{2} y^{2} = 4 b^{2} (x^{2} - a^{2})$