Two concentric ellipses are such that the foci of one are on the other and their major axes are equal. Let eande' be their eccentricities. Then. the quadrilateral formed by joining the foci of the two ellipses is a parallelogram the angle θ between their axes is given by θ=cos−1√1e2+1e'2=1e2e'2 If e2+e'2=1, then the angle between the axes of the two ellipses is 900 none of these
the quadrilateral formed by joining the foci of the two ellipe is a parallelogram
the angle θ between their axes is give by θ=cos−1√1e2+1e'2−1e2e'2
If e2+e'2=1, then the angle between th axes of the two ellipse is 90∘
none of these
Celeary, O is the midpoint of SS' and HH'
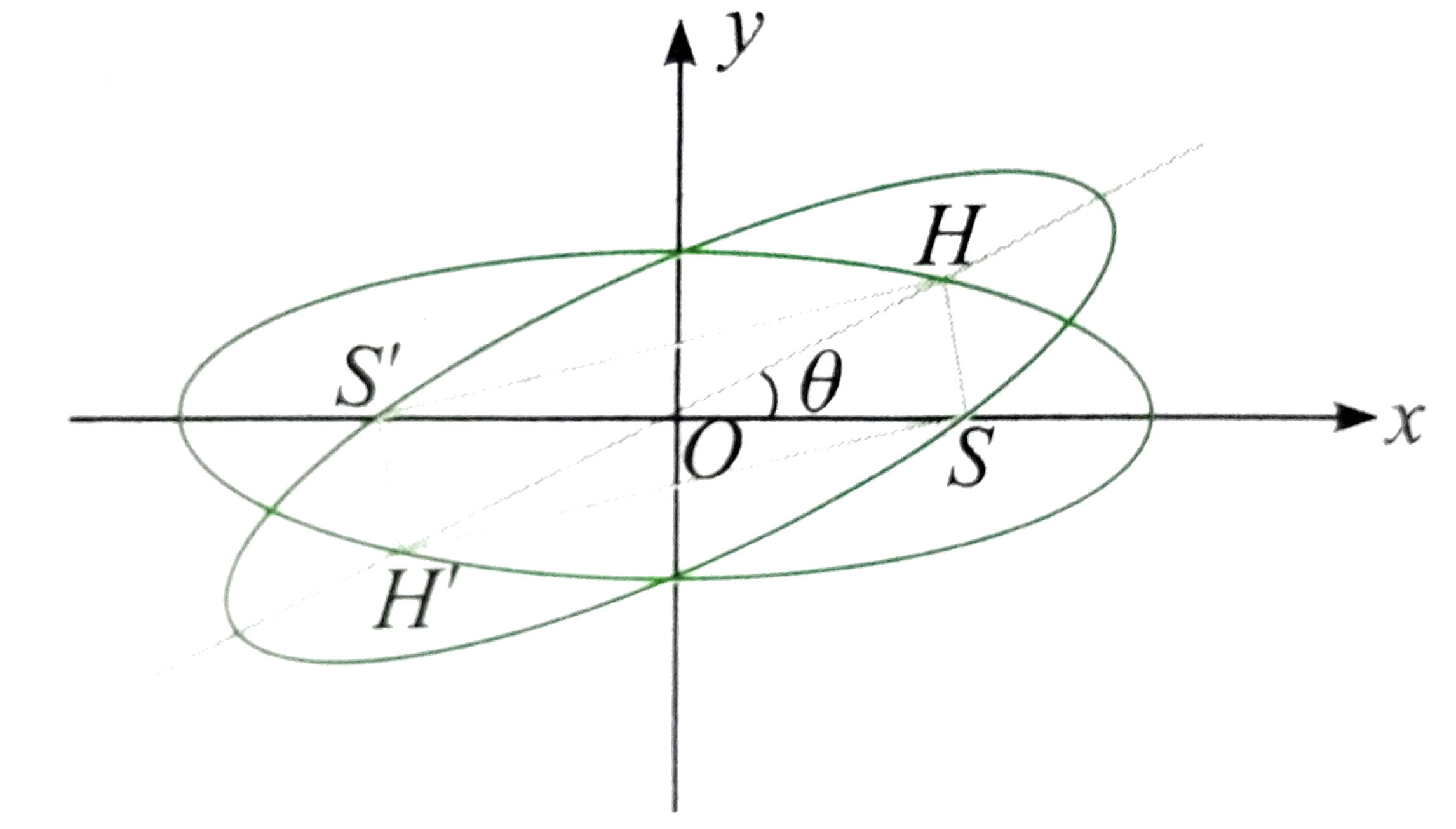
Therfore, the disagonals of quadrilateral HSH'S'' bisect each other. So it is a parallelogram.
The point H lies on
x2a2+y2b2 (Suppose)
∴r2cos2θa2+r2sin2θb2=1
e'2cos2θ+e2sin2θ1−e2=1 [∴b2=a2(1−e2)]
or e'2cos2θ−e'2cos2θ1−e2=1−e'21−e2
or cos2θ1e2+1e'2=1e2e'2
or θ=cos−1√1e2+1e'2−1e2e'2
For θ=90∘,
e2+e'2e2e'2=1e2e'2
ore2+e'2=1
Similar Questions
Two concentric ellipse be such that the foci of one be on the other and if 3/5 and 4/5 be their eccentricities. If theta be the angle between their axes, then the values of 2(1+sin2θ+sin4θ) must be
View SolutionIf two concentric elipse be such that the foci of one be on the and if e and e' be their eccentricities. Prove that the angle between their axes is cos−1{√e2+e'2−1ee'}
View Solution
Knowledge Check
If the length of the semi-major axis of an ellipse is 68 and e = 1/2, then the area of the rectangle formed by joining the vertices of latusrecta of the ellipse is equal to
A69930B6935C6936D3696If e is the eccentricity of x2a2−y2b2=1 & θ be the angle between the asymptotes, then secθ/2 equals
Ae2B1/eC2eDeLet S, S' be the focil and BB' be the minor axis of the ellipse x2a2+y2b2=1. If ∠BSS'=θ, then the eccentricity e of the ellipse is equal to
AsinθBcosθCtanθDcotθ
Find the equation of the ellipse whose foci are at (±1,0)ande=12.
View SolutionThe eccentricity of an ellipse is 12 and the distance between its foci is 4 units. If the major and minor axes of the ellipse are respectively along the xandy axes, find the equation of the ellipse.
View SolutionThe eccentricity of an ellipse is 12 and the distance between its foci is 4 units. If the major and minor axes of the ellipse are respectively along the xandy axes, find the equation of the ellipse
View SolutionIf e is the eccentricity of x2a2−y2b2=1 and θ be the angle between its asymptotes, then cos(θ2) is equal to
View SolutionIf e is the eccentricity of the hyperbola x2a2−y2b2=1 and θ is the angle between the asymptotes, then cos.θ2 is equal to
View Solution
