The length of the tangent of the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{16} = 1$ intercepted between auxiliary circle such that the portionof the tangent intercepted between the auxiliary circle subtends equal angles at foci is

Video Solution

Text Solution

Verified by Experts

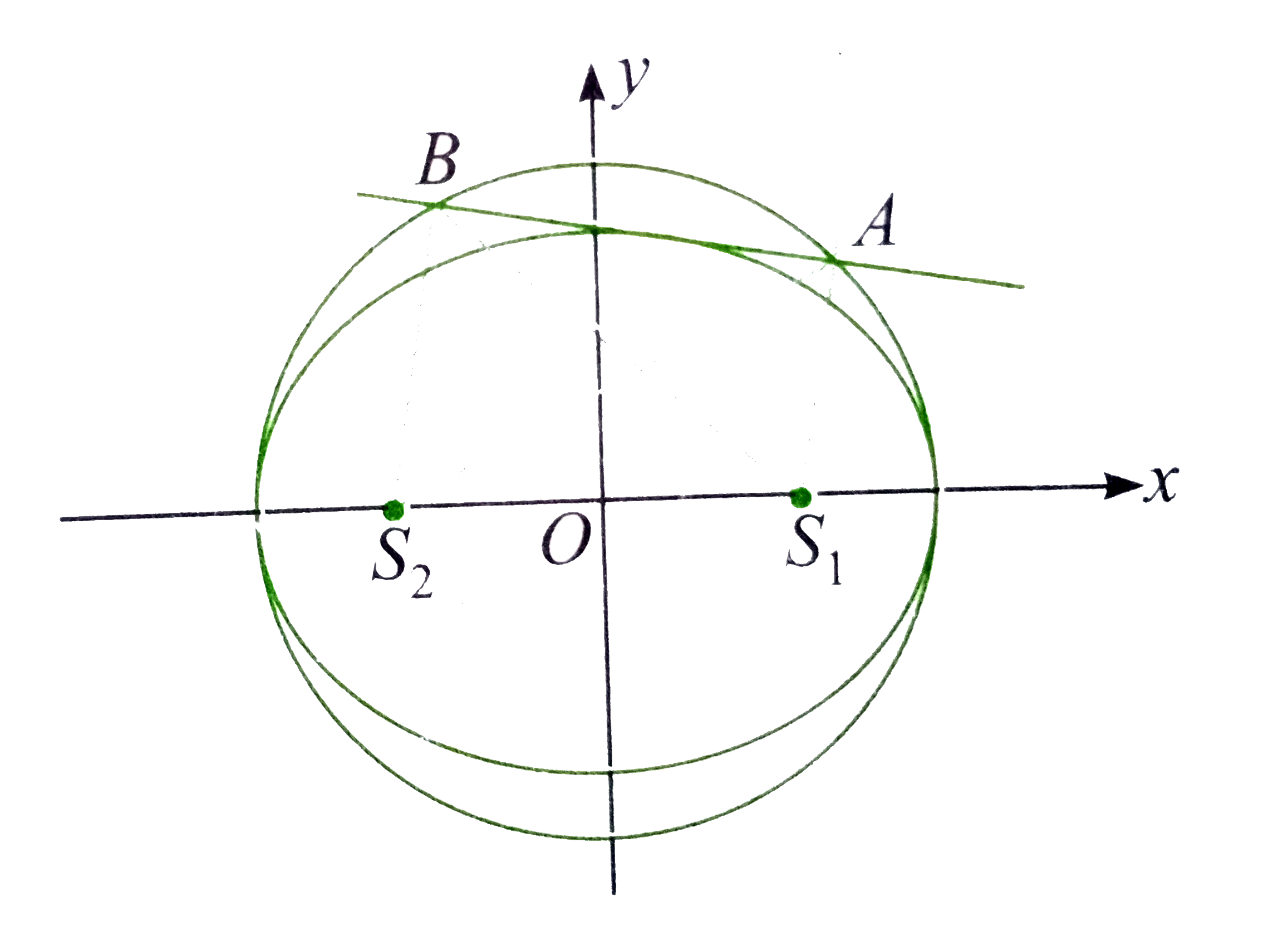
Let AB be the length of the tangent intercepted by auxiliary circle and $S_{1}, S_{2}$ be the foci.
Given that
$∠ A S_{1} B = ∠ A S_{2} B$
$\Rightarrow ∠ S_{1} A B = ∠ S_{2} A B = \frac{π}{2}$
So $A S_{1} S_{2} B$ is a rectangle.
$∴ A B = S_{1} S_{2} = 2 a e x = 2 \times 5 \times \frac{3}{5} = 6$

Updated on:21/07/2023

If any tangent to the ellipse $\frac{x^{2}}{16} + \frac{y^{2}}{9} = 1$ intercepts equal lengths l on the both axis, then l =
A $3$
B $5$
C $\sqrt{5}$
DNone of these
The length of the common tangent to the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{4}$ = 1 and the circle $x^{2} + y^{2} = 16$ intercepted by
A5
B $2 \sqrt{7}$
C $\frac{7}{\sqrt{3}}$
D $\frac{14}{\sqrt{3}}$
The portion of the tangent of the curve $x^{\frac{2}{3}} + y^{\frac{2}{3}} = a^{\frac{2}{3}}$ ,which is intercepted between the axes is (a>0)
Aa
B2a
C3a
Dnone