Tangents are drawn to the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1, (a > b),$ and the circle $x^{2} + y^{2} = a^{2}$ at the points where a common ordinate cuts them (on the same side of the x-axis). Then the greatest acute angle between these tangents is given by ${tan}^{- 1} (\frac{a - b}{2 \sqrt{a b}})$ (b) ${tan}^{- 1} (\frac{a + b}{2 \sqrt{a b}})$ ${tan}^{- 1} (\frac{2 a b}{\sqrt{a - b}})$ (d) ${tan}^{- 1} (\frac{2 a b}{\sqrt{a + b}})$

${tan}^{- 1} (\frac{a - b}{2 \sqrt{a b}})$

${tan}^{- 1} (\frac{a + b}{2 \sqrt{a b}})$

${tan}^{- 1} (\frac{2 a b}{2 \sqrt{a - b}})$

${tan}^{- 1} (\frac{2 a b}{2 \sqrt{a + b}})$

Video Solution

Text Solution

Verified by Experts

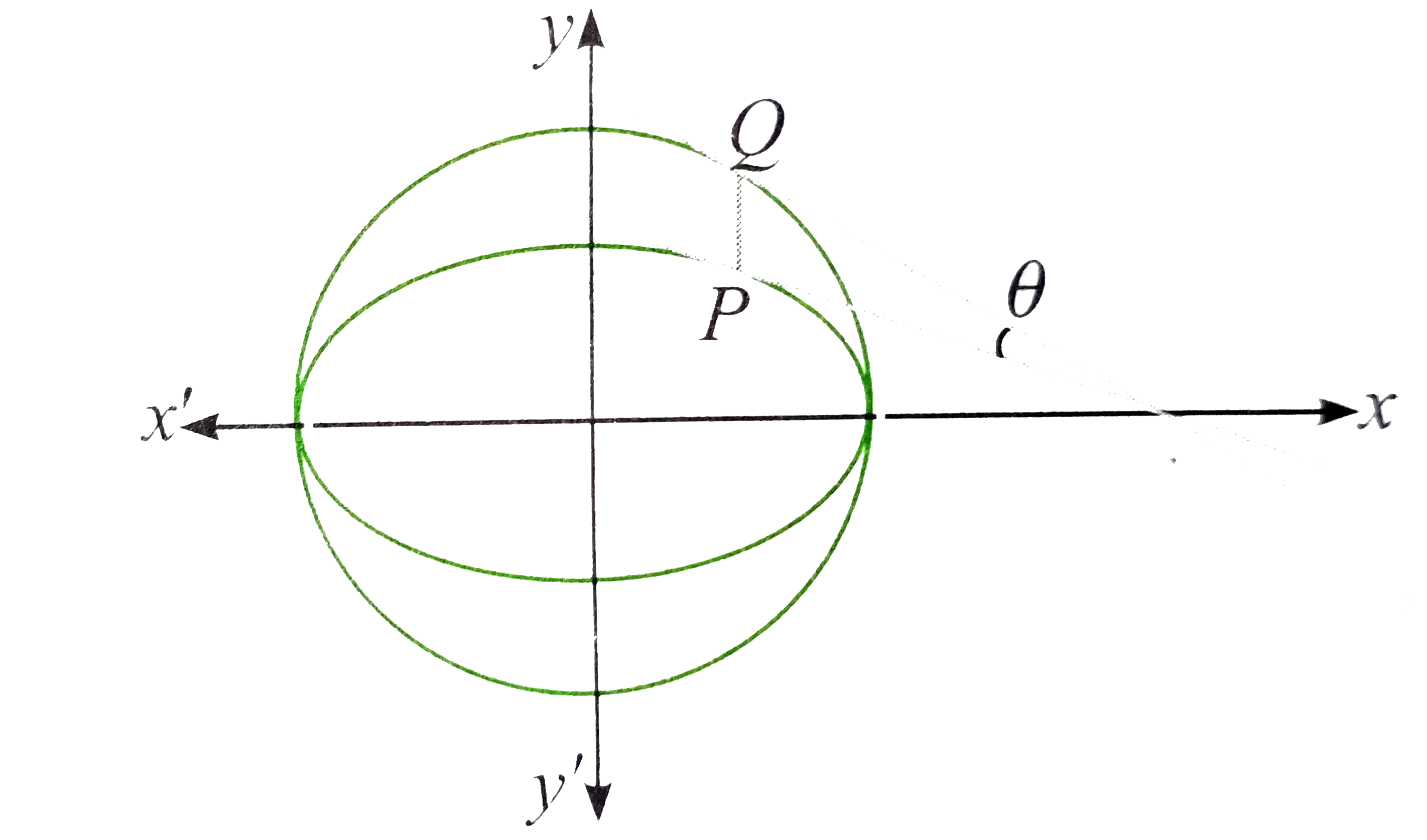
Tanent to the ellipse at $P (a cos α, b sin α)$ is $\frac{x}{a} cos α + \frac{y}{b} i s n α = 1 (1)$
Tangent to the circle at $Q (a cos, α, a sin α)$ is $cos a x + sin α y = a (2)$
Now, the angle between the tangents is $θ$ . Then, $tan θ = ∣ ∣ ∣ ∣ ∣ \frac{- \frac{b}{a} cot α - (- cot α)}{1 + (- \frac{b}{a} cot α) (- cot α)} ∣ ∣ ∣ ∣ ∣$
$= ∣ ∣ ∣ ∣ ∣ \frac{cos α (1 - \frac{b}{a})}{1 + \frac{b}{a} {cot}^{2} α} ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ \frac{a - b}{a tan α + b cot α} ∣ ∣ ∣$
$= ∣ ∣ ∣ ∣ ∣ \frac{a - b}{{(\sqrt{a tan α} - \sqrt{b cot α})}^{2} + 2 \sqrt{a b}} ∣ ∣ ∣ ∣ ∣$
Now, the greatest value of the above expression is $∣ ∣ ∣ \frac{a - b}{2 \sqrt{a b}} ∣ ∣ ∣$ when $\sqrt{tan α} = \sqrt{b tan α}$ . Therefore,
$θ_{maximum} = {tan}^{- 1} (\frac{a - b}{2 \sqrt{a b}})$

Updated on:21/07/2023

If $\frac{x}{a} + \frac{y}{b} = \sqrt{2}$ touches the ellipse $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ at a point P, then eccentric angle of P is
A $0$
B $45^{\circ}$
C $60^{\circ}$
D $90^{\circ}$