The area of the quadrilateral formed by the tangents at the endpoint of the latuc rectum to the ellipse x29+y025=1 is 27/4 sq. unit (b) 9 sq. units 27/2 sq. unit (d) 27 sq. unit
27/4 sq units
9 sq. units
27/2 sq .units
27 sq.units
The given ellipse is
x29+y25=1
Then , a2=9,b2=5. Therefore,
e=√1−59=23
The equation of tangent at L is 2x9+y3=1
The tangent meets rthe x-axis at A(9/2,0) and the y-axis at B(0,3) . Therefore,
Area of ΔOAB=12×92×3=274
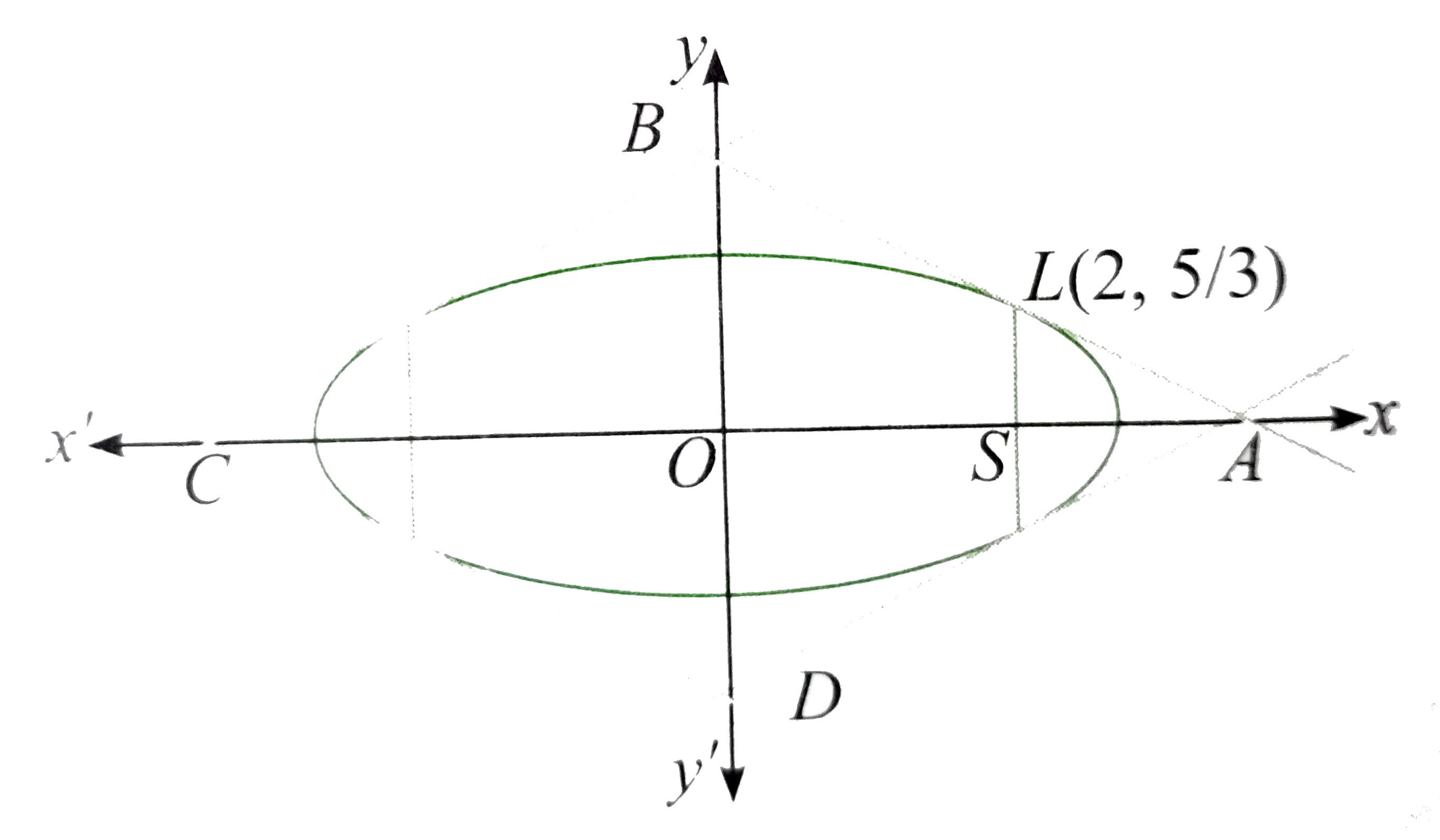
By symmetry,
Area of quadrilateral =4×(Area of ΔOAB)
=4×274=27 sq. units
Similar Questions
The area of the quadrilateral formed by the tangents at the endpoint of the latus rectum to the ellipse x29+y25=1 is (A) 274 sq. unit (B) 9 sq. units (C) 272 sq. unit (D) 27 sq. unit
View SolutionThe area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latera recta to the ellipse x29+y25=1 , is: (1) 274 (2) 18 (3) 272 (4) 27
View SolutionArea of the triangle formed by the line x+y=3 and the angle bisectors of the pairs of straight lines x2−y2+2y=1 is 2sq.units (b) 4sq.units 6sq.units (d) 8sq.units
View SolutionThe area (in sq. units) of the triangle formed by the latus rectum and the tangents at the end points of the latus rectum of x216−y29=1 is equal to
View SolutionArea of the triangle formed by the x+y=3 and angle bisectors of the pair of straight lines x2−y2+2y=1 is 2 sq. units (b) 4 sq. units 6 sq. units (d) 8 sq. units.
View SolutionThe area enclosed by 2|x|+3|y|≤6 is (a)3 sq. units (b) 4 sq. units (c)12 sq. units (d) 24 sq. units
View SolutionThangents are drawn from (−1,0) to y2=4x. Then the area of the triangle fromed by the tangents and the chord of the contact is : (A) 8 sq. units (B) 2 sq. units (C) 4 sq. units (D) 1 sq.units
View SolutionThe area of a sector whose perimeter is four times its radius r units, is (a) r24 sq. units (b) 2r2 sq. units (c) r2 sq. units (d) r22 sq. units
View SolutionThe tangents at the extremities of the latus rectum of the ellipse 3x2+4y2=12 form a rhombus PQRS. Area (in sq. units) of the rhombus PQRS outside and ellipse is equal to
View SolutionIf the area of the triangle is 4sq units, then x is
View Solution
