The point of intersection of the tangents at the point P on the ellipse x2a2+y2b2=1 and its corresponding point Q on the auxiliary circle meet on the line x=ae (b) x=0 y=0 (d) none of these
x=a/e
x=0
y=0
none of these
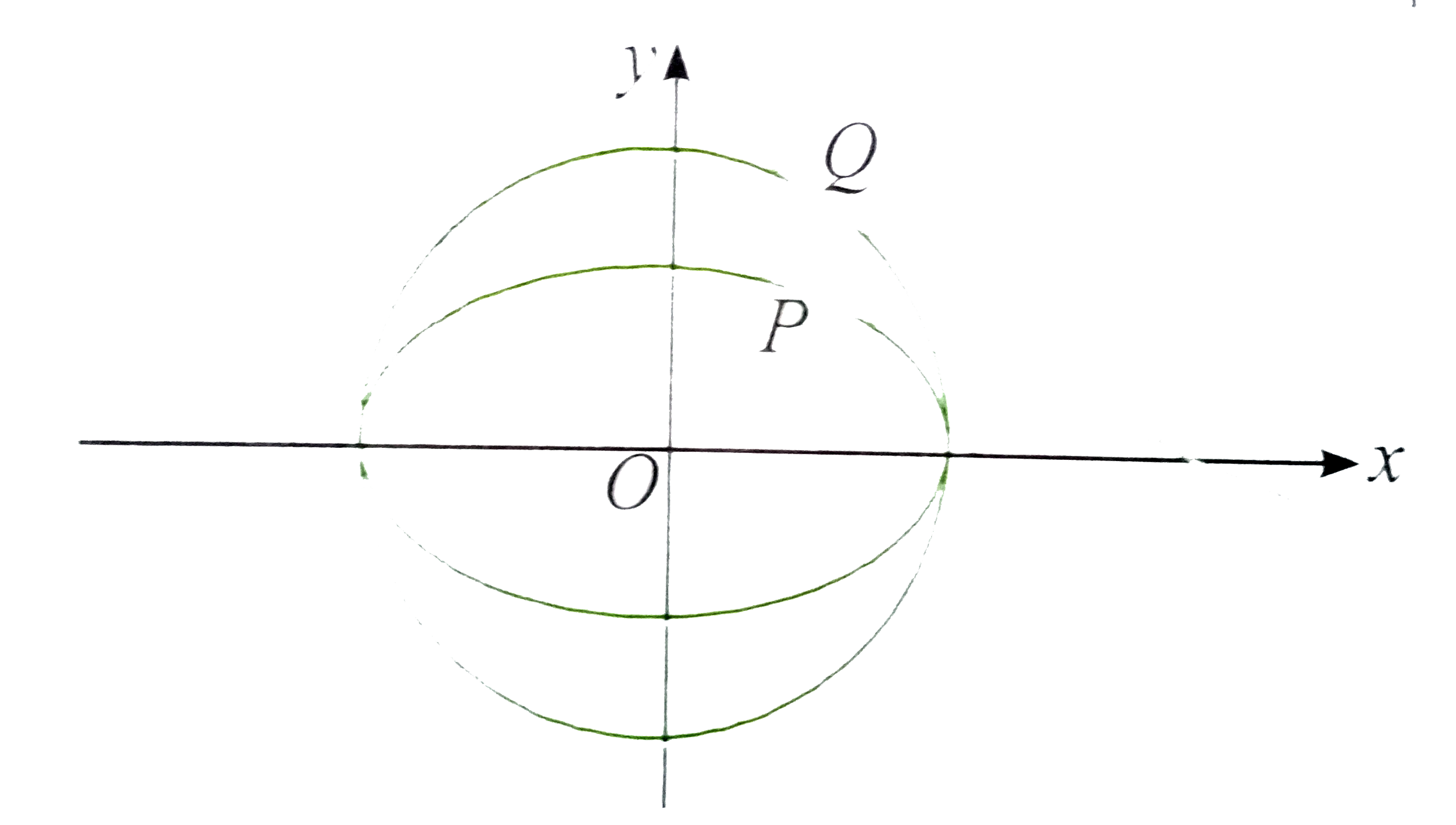
Tangent to the ellipse at point P(acosθ,asinθ) is xacosthea+ybsinθ=1(1)
Tangent (1) and (2) intersect at (a/cosθ,0) which lies on y=0
Similar Questions
Knowledge Check
the locus of the point of intersection of tangents to the ellipse x2a2+y2b2=1 which meet at right , is
Aa circleBa parabolaCan ellipseDa hyperbolaThe line x=at2 meets the ellipse x2a2+y2b2=1 in the real points if
A|t|<2B|t|≤1C|t|>1Dnone of the aboveThe line x=at2 meets the ellipse x2a2+y2b2=1 in the real points if
A|t|<2B|t|≤1C|t|>1Dnone of the above
Let a tangent at a point P to the ellipse x2a2+y2b2=1 meets directrix at Q and S be the correspondsfocus then ∠PSQ
View SolutionP is a point on the ellipse x225+y29 and Q is corresponding point of P on its auxiliary circle. Then the locus of point of intersection of normals at P & Q to the respective curves is
View SolutionThe locus of the point of intersection of the tangent at the endpoints of the focal chord of the ellipse x2a2+y2b2=1(b<a)(a) is a an circle (b) ellipse (c) hyperbola (d) pair of straight lines
View SolutionLocus of point of intersection of perpendicular tangents to the circle x2+y2−4x−6y−1=0 is
View SolutionP is a point on the ellipse E:x2a2+y2b2=1 and P' be the corresponding point on the auxiliary circle C:x2+y2=a2 . The normal at P to E and at P' to C intersect on circle whose radius is
View Solution
