With a given point and line as focus and directrix, a series of ellipses are described. The locus of the extremities of their minor axis is an ellipse (b) a parabola a hyperbola (d) none of these
an ellipse
a parabola
a hyperbola
none of these
Let S be the given focus and ZM be the given directrix. Then,
SZ=ae−ae
=ae(1−e2)
=b2aek (say)
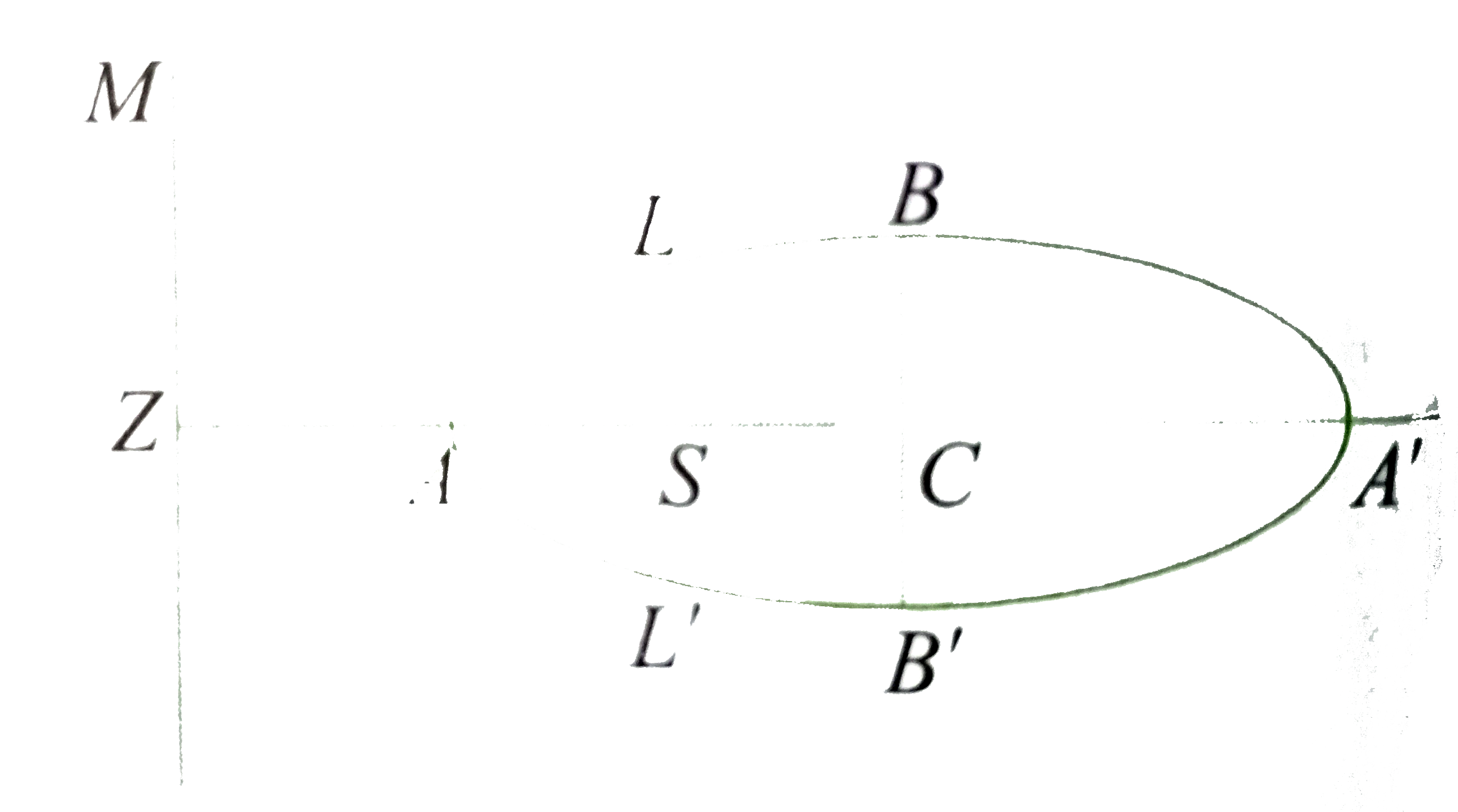
Now, take SC as the x-axis and LS'L as the y-axis . Let (x,y() be the coordinaters of B with respect to these axes. Then , x=SC=ae and y =CB=b b. Hence,
x2a2=b2ae=SZ
Which is constan.
Therefore, y2=kx is the required locus which is a parabola.
Similar Questions
With a given point and line as focus and directrix, a series of ellipses are described. The locus of the extremities of their minor axis is an (a)ellipse (b)a parabola (c)a hyperbola (d)none of these
View SolutionLocus of the centre of the circle touching circles |z|=3and|z−4|=1 externally is (A) a parabola (B) a hyperbola (C) an ellipse (D) none of these
View Solution
Knowledge Check
IF the distance between a focus and corresponding directrix of an ellipse be 8 and the eccentricity be 12, then length of the minor axis is
A3B4√2C6D16√33If the distance betweent a focus and corresponding directrix of an ellipse be 8 and the eccentricity be 12, then length of the minor axis is
A3B4√2C6D16√33Variable ellipses are drawn with x=−4 as a directrix and origin as corresponding foci. The locus of extremities of minor axes of these ellipses is:
Ay2=4xBy2=2xCy2=xDx2=4y
A circle touches the x-axis and also thouches the circle with center (0, 3) and radius 2. The locus of the center of the circle is a circle (b) an ellipse a parabola (d) a hyperbola
View SolutionThe curve in the first quadrant for which the normal at any point (x,y) and the line joining the origin to that point form an isosceles triangle with the x-axis as base is (a) an ellipse (b) a rectangular hyperbola (c) a circle (d) None of these
View SolutionIf a hyperbola passes through the foci of the ellipse x225+y216=1 . Its transverse and conjugate axes coincide respectively with the major and minor axes of the ellipse and if the product of eccentricities of hyperbola and ellipse is 1 then the equation of a. hyperbola is x29−y216=1 b. the equation of hyperbola is x29−y225=1 c. focus of hyperbola is (5, 0) d. focus of hyperbola is (5√3,0)
View SolutionIf the normal at an end of a latus rectaum of an ellipse passes through an extremity of the minor axis then the eccentricity of the ellispe satisfies .
View SolutionIn an ellipse, if the lines joining focus to the extremities of the minor axis form an equilateral triangle with the minor axis, then the eccentricity of the ellipse is
View Solution
