Tangents PQandPR are drawn at the extremities of the chord of the ellipse x216+y29=1 , which get bisected at point P(1,1). Then find the point of intersection of the tangents.
The correct Answer is:(14425,14425)
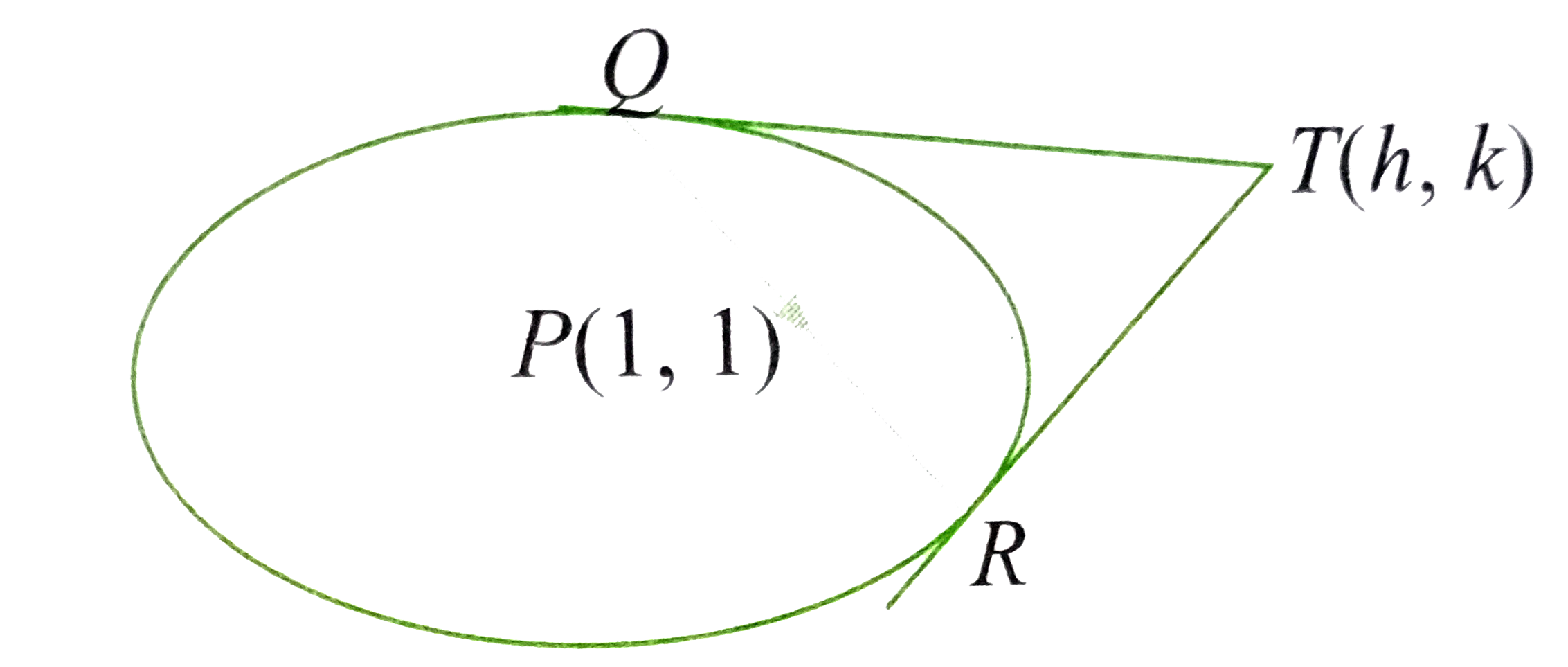
Eqution of chord having midpoint P(1,1) is
1⋅x16+1⋅y9−1=116+19−1
or x16+y9=25144
or9x+16y=25(1)
Also, line QR is chord of contact w.r.t. point (h,k).
It equations is
hx16+ky9=1
or 9hx+16ky=144 (2)
Equatiosn (1) and (2) represent the same stragith line.
∴9h9=16k16=14425
⇒(h,k)≡(14425,14425)
Similar Questions
Tangents PQandPR are drawn at the extremities of the chord of the ellipse x216+y29=1 , which get bisected at point P(1,1). Then find the point of intersection of the tangents.
View SolutionA chord PQ of the ellipse x29+y24=1 subtends a right angle at the centre of the ellipse. The locus of the point of intersection of the tangents to the ellipse at P and Q is .......
View Solution
Knowledge Check
Tangents are drawn to ellipse x2a2+y2b2=1 at points P(θ1) and Q(θ2) then the point of intersection of these tangents is
A⎛⎜⎝acosθ1+θ22cosθ1−θ22,b sinθ1+θ22cosθ1−θ22⎞⎟⎠B⎛⎜⎝acosθ1−θ22cosθ1+θ22,b sinθ1−θ22cosθ1+θ22⎞⎟⎠C⎛⎜⎝a sinθ1+θ22sinθ1−θ22,b cosθ1+θ22sinθ1−θ22⎞⎟⎠DnoneThe mid point of the chord 16x+9y=25 to the ellipse x29+y216=1 is
A(1,-1)B(-1,1)C(-1,1)D(1,1)If tangents are drawn from any point on the circle x2+y2=25 to the ellipse x216+y29=1, then the angle between the tangents is
A2π3Bπ4Cπ3Dπ2
Tangents are drawn from the point P(3, 4) to the ellipse x29+y24=1 touching the ellipse at points A and B.
View SolutionNumber of tangents that can be drawn from the point (4√t,3(t−1)) to the ellipse x216+y29=1
View SolutionIf PQ is the focal chord of the parabola y2=−xandP is (−4,2), then the ordinate of the point of intersection of the tangents at P and Q is
View SolutionIf 3x+4y=12 intersect the ellipse x225+y216=1 at P and Q , then point of intersection of tangents at P and Q.
View SolutionThe sum of the slopes of the tangents to the ellipse x29+y24=1drawn from the point (6,-2) is
View Solution