An ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is (A) √3 (B) 2 (C) 2√2 (D) √5
The correct Answer is:2
Givemn ellipse
x225+y216=1
∴E2=1−1625ore=35
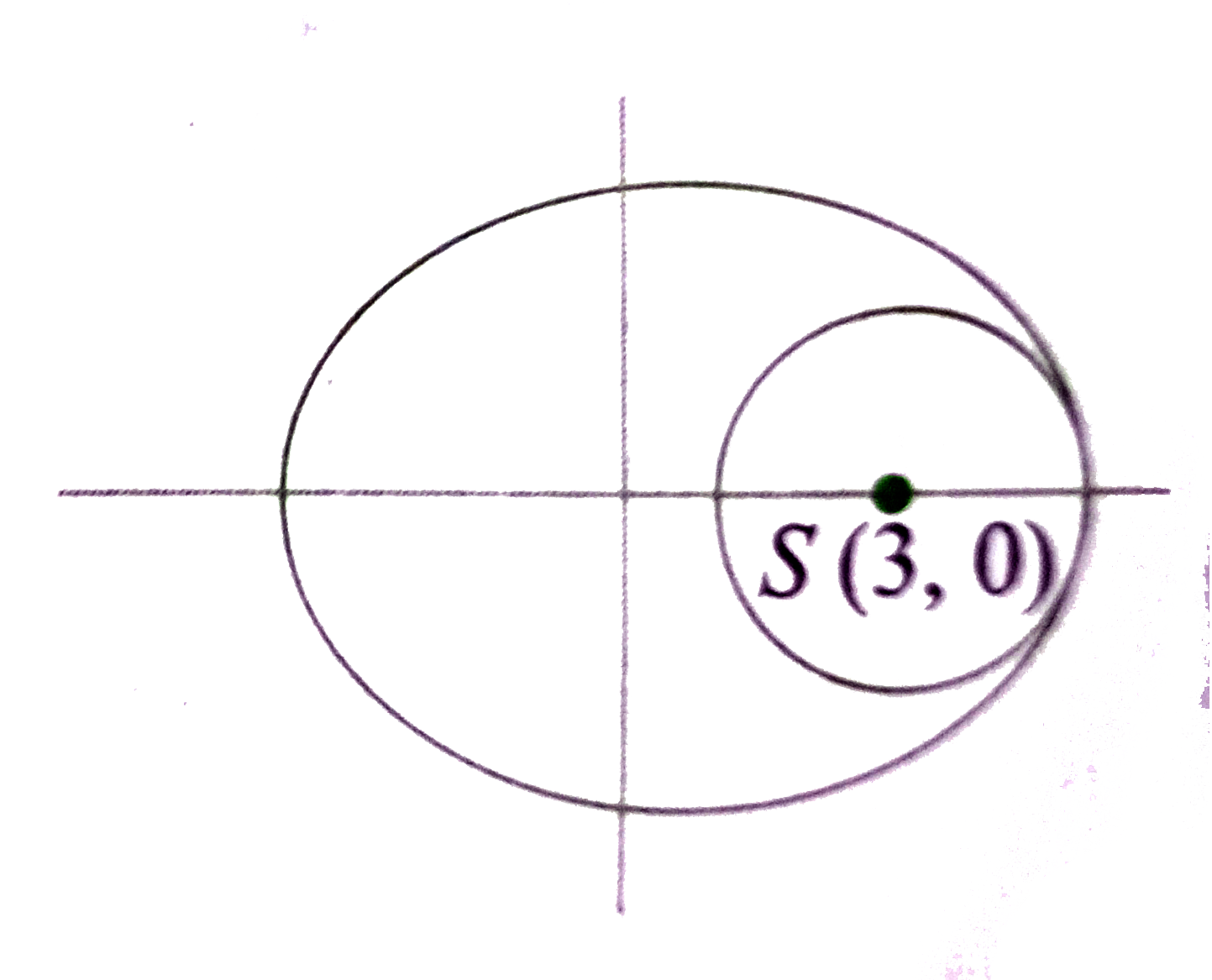
then foci are (±ae,0)≡(±3,0)
Now, the circle having center (3,0) is
(x−3)2+y2=r2
Eliminating y2 from (1) and (2), we get
16x2+25r2−25(x2−6x+9)=400
or −9x2+150x+25r2−625=0
since the circle touches the ellipse, the above equation, has equal roots. Hence D=0,i.e.,22500+36(25r2−625)=0, which is not possible
Then the circle will touche the ellipse at the end of the major axis, (5,0) Hence, the radius is 2
Similar Questions
An ellipse is drawn with major and minor axis of length 10 and 8 respectively. Using one focus a centre, a circle is drawn that is tangent to ellipse, with no part of the circle being outside the ellipse. The radius of the circle is (A) √3 (B) 2 (C) 2√2 (D) √5
View SolutionWith one focus of the hyperbola x29−y216=1 as the centre, a circle is drawn which is tangent to the hyperbola with no part of the circle being outside the hyperbola. The radius of the circle is
View Solution
Knowledge Check
- Question 1 - Select One
An ellipse of major and minor axes of length √3 and 1 respectively, slides along the coordinate axes and alwys remains confined in the first quadrant. The locus of the centre of the ellipse will be the arec of a circle. The length of the arc is
AπBπ2Cπ3Dπ6 - Question 2 - Select One
The lengths of major and minor axis of an ellipse are 10 and 8 respectively and its major axis is along the Y-axis. The equation of the ellipse referred to its centre as origin is
Ax225+y216=1Bx216+y225=1Cx2100+y264=1Dx264+y2100=1 - Question 3 - Select One
Let x+6y=8 is tangent to standard ellipse where minor axis is 4√3, then eccentricity of ellipse is
A√56B√1112C(13)√113D(14)√1112
The line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4. The radius of the circle is 3√5 (b) 5√3 (c) 2√5 (d) 5√2
View SolutionThe major and minor axes of an ellipse are along x,y axis respectively. If its latusrectum is of length 4 and the distance between the foci is 4√2 then the equation of that ellipse
View SolutionA circle is drawn whose centre is on the x - axis and it touches the y - axis. If no part of the circle lies outside the parabola y2=8x, then the maximum possible radius of the circle is
View SolutionIn an ellipse the distance between the foci is 8 and the distance between the directrices is 25. The length of major axis is : (A) 5√2 (B) 10√2 (C) 20√2 (D) none of these
View SolutionWhat is the length of the perpendicular drawn from the centre of circle of radius r on the chord of length √3
View Solution

