Tangent are drawn from the point (3, 2) to the ellipse $x^{2} + 4 y^{2} = 9$ . Find the equation to their chord of contact and the middle point of this chord of contact.

Video Solution

Text Solution

Verified by Experts

$x^{2} + 4 y^{2} = 9$
The equatin of the chord of contact of the pair of tangents from (3,2) is $3 x + 8 y = 9 (1)$

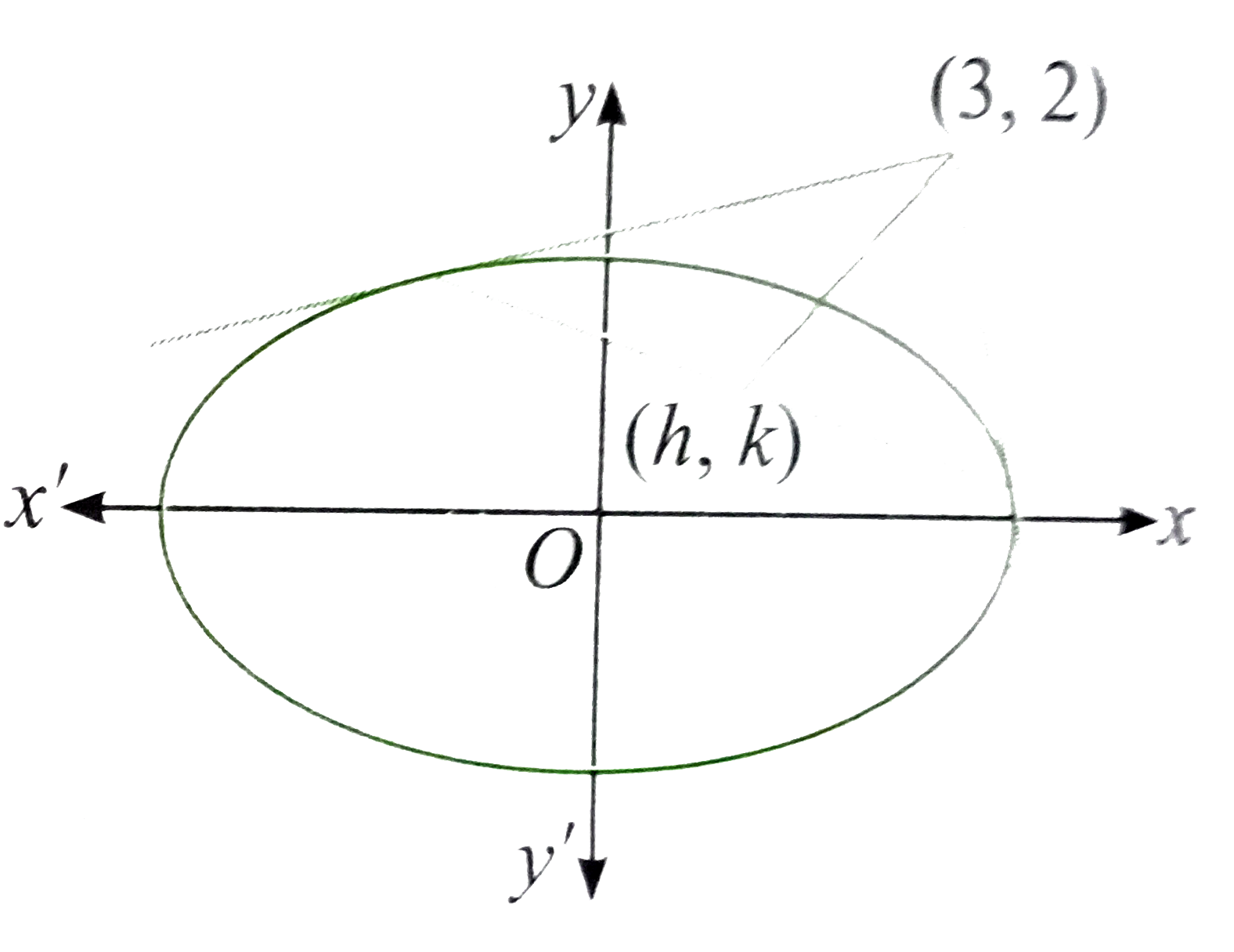
This mut be the same as the chord whose middle point is (h,k)
$T = S_{1}$
$\frac{h x}{9} + \frac{k y}{9 / 4} = \frac{h^{2}}{9} + \frac{k^{2}}{9 / 4}$
or hx+4ky= $h^{2} + 4 k^{2} (2)$
Equation (1) and (2) represent the same straight lines.
Comparing the coefficients of (1) and (2) , we get
$\frac{h}{3} = \frac{4 k}{8} = \frac{h^{2} + 4 k^{2}}{9}$
$or 2 h = 3 k and 3 h = h^{2} + 4 k^{2}$
or $3 h = h^{2} + 4 \times \frac{4 h^{2}}{9}$
or $\frac{25 h^{2}}{9} = 3 h$
or $h = \frac{27}{25} and k = \frac{18}{25}$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Similar Questions

Knowledge Check

Tangents are drawn from any point on the line $x + 4 a = 0$ to the parabola $y^{2} = 4 a x$ The angle subtanded by their chord of contact at the vertex is
A $π / 3$
B $π / 4$
C $π / 2$
Dnone

Recommended Questions

Home
Ask Doubt
Profile