Question

Two circles are given such that one is completely
lying inside the other without touching. Prove that the locus of the center
of variable circle which touches the smaller circle from outside and the
bigger circle from inside is an ellipse.

Explanation

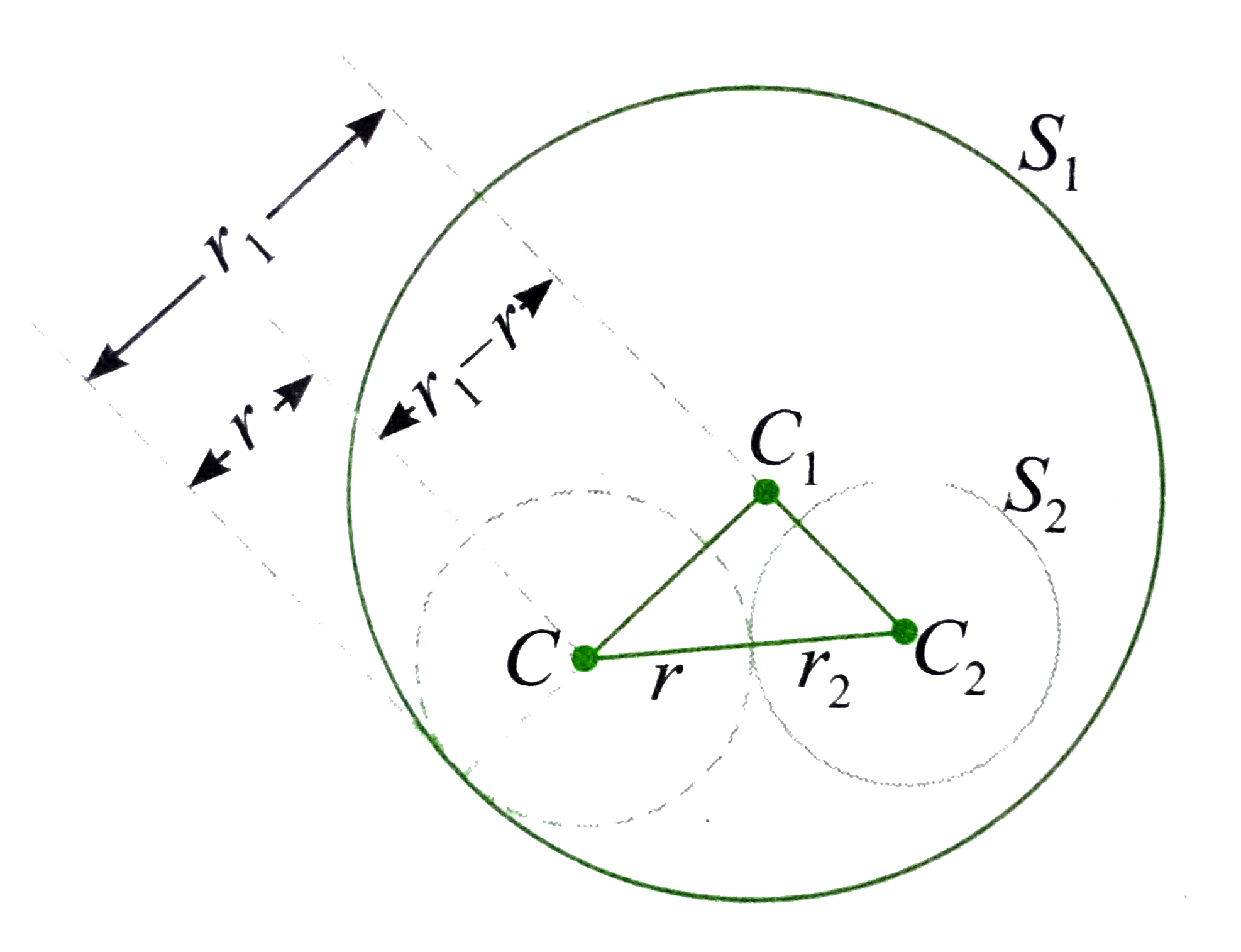
Let the circle `S_(2)` having centre at `C_(2)` and redius `r_(2)` lie completely insid the circle `S_(1)` having centre at `C_(1)` and radius `r_(1)`
Variable circle S touches `S_(1)` intrnally and `S_(2)` externally. Centre C of circle S is variable point and its radius 'r' is also variable. From the figure `C C_(2)=r+r_(2) and C C_(1) =r_(1)-r` So, `C C_(1)+ C C_(2)=r_(1)+r_(2)` (constant) Thus, locus of C is ellips whose foci are at `C_(1) and C_(2)`