Let $T_{1}, T_{2}$ and be two tangents drawn from (-2, 0) onto the circle $C : x^{2} + y^{2} = 1$ . Determine the circles touching C and having $T_{1}, T_{2}$ as their pair of tangents. Further, find the equations of all possible common tangents to these circles when taken two at a time

Video Solution

Text Solution

Verified by Experts

The given circle is
$x^{2} + y^{2} = 1$ (1)
Center $\equiv O (0, 0)$ and radius $= 1$
Let $T_{1}$ and $T_{2}$ be the tangents drawn from $(- 2, 0)$ to the circle (1) .

From the figure, $Δ P L O$ and $Δ P M C_{1}$ are similar. Therefore,
$\frac{O L}{O P} = \frac{C_{1} M}{C_{1} P}$
or $\frac{1}{2} = \frac{r_{1}}{h_{1} + 2}$
or $2 r_{1} = h_{1} + 2$ (2)
Also, the circle are touching externally. Therefore,
$h_{1} = r_{1} + 1$ (3)
From (2) and(3),
$r_{1} = 3$ and $h_{1} = 4$
Hence, $Δ P L O$ and $Δ P N C_{2}$ are similar. Therefore,
$\frac{O L}{O P} = \frac{C_{2} N}{C_{2} P}$
or $\frac{1}{2} = \frac{r_{2}}{2 + h_{2}}$
or $2 r_{2} = 2 + h_{2}$ (5)
Also, the circles are touching externally. Therefore,
$- h_{2} = 1 + r_{2}$ (6)
From (5) and (6)
${(x + \frac{4}{3})}^{2} + y^{2} = {(\frac{1}{3})}^{2}$ (7)
Since circles (1) and (4) are two touching circles, they have three common tangents $: T_{1}, T_{2},$ and $x - 1 = 0$ .
Similarly, the common tangents of circles (1) and (7) are $T_{1}, T_{2}$ , and $x = - 1$ .

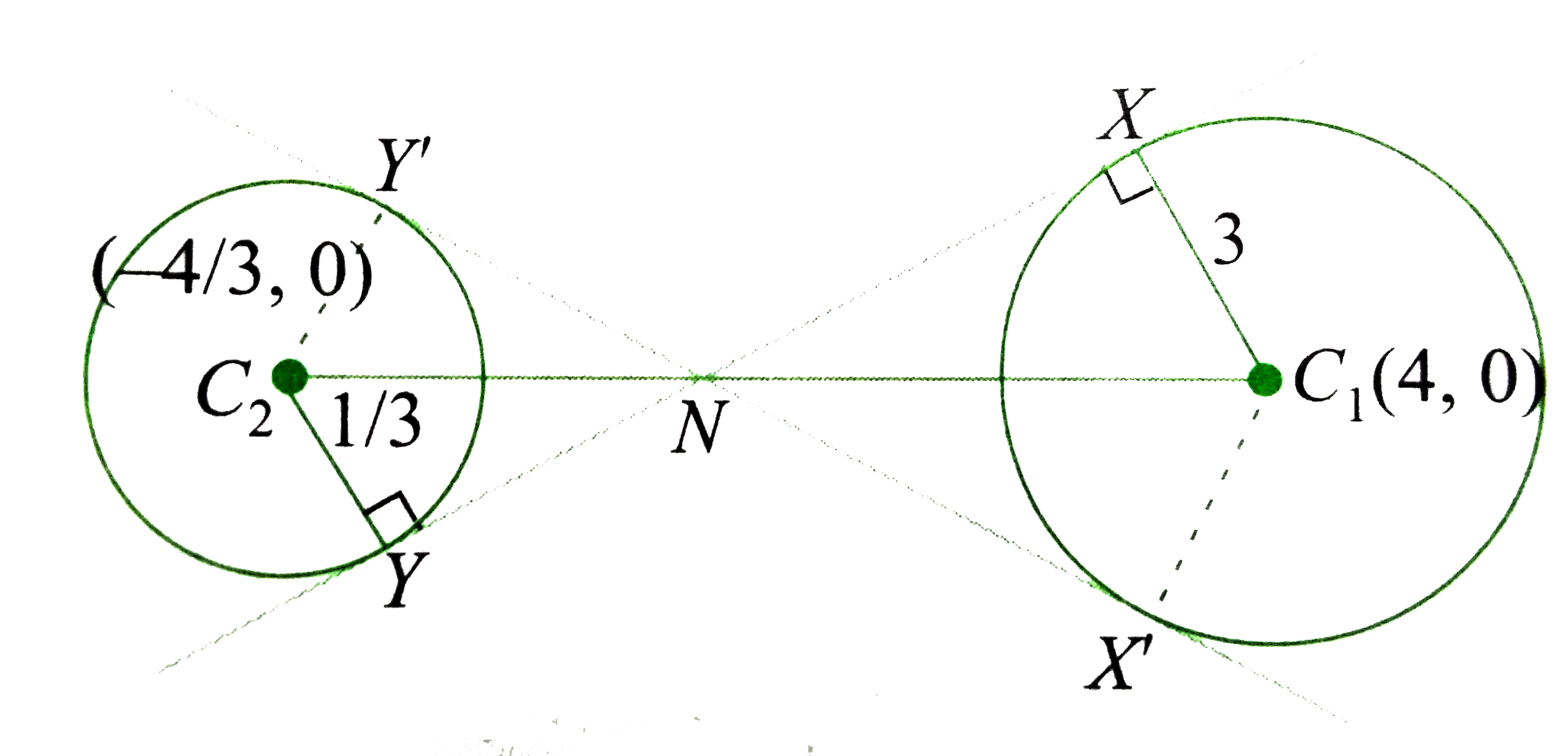
For the circles (4) and (7) , there will be four common tangnets $:$ two direct and two indirect.
Two common direct tangents $T_{1}$ and $T_{2}$ .
Let common direct are $T_{1}$ and $T_{2}$
Let us find two common indirect tangents.
$\frac{C_{1} N}{C_{2} N} = \frac{3}{1 / 3} = 9$
i.e., N divides $C_{1} C_{2}$ in the ratio $9 : 1$ . Therefore,
$N \equiv (\frac{9 \times (- 4 / 3) + 1 \times 4}{10}, 0) \equiv (\frac{- 4}{5}, 0)$
Any line through N is
$y = m (x + \frac{4}{5})$
or $5 m x - 5 y + 4 m = 0$
If it is tangent to circle (4), then
$∣ ∣ ∣ \frac{20 m + 4 m}{\sqrt{25 m^{2} + 25}} ∣ ∣ ∣ = 3$
or $24 m = 15 \sqrt{m^{2} + 1}$
or $64 m^{2} = 25 m^{2} + 25$
or $39 m^{2} = 25 m^{2} + 25$
or $m = \pm \frac{5}{\sqrt{39}}$
Therefore, the required tangents are
$y = \pm \frac{5}{\sqrt{39}} (x + \frac{4}{5})$

Updated on:21/07/2023

The equation of pair of tangents to the circle $x^{2} + y^{2} = 16$ drawn from the point (1,4) is
A $x^{2} + y^{2} - x - 4 y = 0$
B $x^{2} + y^{2} + x - 4 y = 0$
C $x^{2} + y^{2} - 2 x - 8 y = 0$
DNone of these
The equation of tangents drawn from the point (0,1) to the circle $x^{2} + y^{2} - 4 x - 2 y + 4 = 0$ are
A2x-y+1=0 ,x+2y-2=0
B2x-y-1=0 ,x+2y-2=0
C2x-y+1=0,x+2y+2=0
D $x = \pm \sqrt{3} (y - 1)$
If two tangents are drawn from a point to the circle $x^{2} + y^{2} = 32$ to the circle $x^{2} + y^{2} = 16$ , then the angle between the tangents is
A $\frac{- π}{4}$
B $\frac{π}{3}$
C $\frac{π}{2}$
D $\frac{π}{6}$