Find the equations of the circles which pass through the origin and cut off chords of length a from each of the lines y=xandy=−x
The correct Answer is:x2+y2±√2ax=0 and x2+y2±√2ay=0
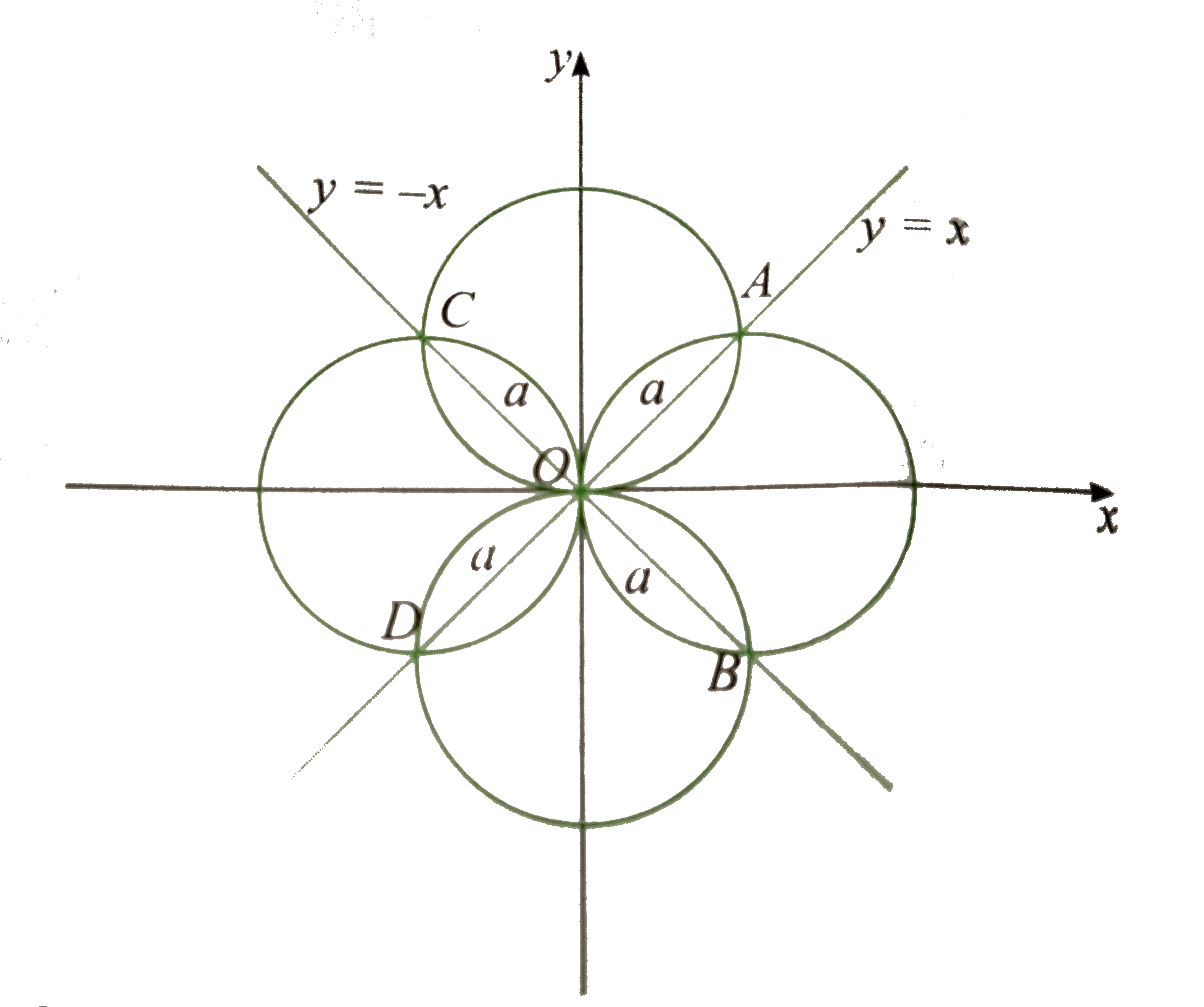
In the figure, length of chords OA and AB that cut off by the circles is a.
∴A≡(a√2,a√2) and B≡(a√2,−a√2), which are end points of diameters.
Therefore, the equation of circle is
(x−a√2)(x−a√2)+(y−a√2)(y+a√2)=0
or x2+y2−√2ax=0
Circles with AC and BD as diametere are given by x2+y2±√2ay=0
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.3
18 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.4
14 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.1
14 Videos
- BINOMIAL THEORMBOOK - CENGAGECHAPTER - BINOMIAL THEORMEXERCISE - Question Bank
31 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
Similar Questions
Knowledge Check
Equation of the circle which passes through the origin and cuts off intercepts of length 2 units from negative co-ordinate axes , is
Ax2+y2+2x+2y=0Bx2+y2+2x−2y=0Cx2+y2+2x+2y=0Dx2+y2−2x−2y=0Equation to the circles which pass through the point (2,3) and cut off equal chords of length 6 units along the lines y-x-1=0 and y+x-5=0 is
A(x−3)2+(y−2√3)2=(3√2)2B(x−2)2+(y−3−3√2)2=(3√2)2C(x−2√3)2+(y−3)2=(3√2)2Dnone of these
Find the equation of the circle which passes through the origin and cut off equal chords of √2 units from the lines y=xandy=−x.
View SolutionFind the equation of the circle , which passes through the origin and cuts off intercepts a and b from the axes.
View SolutionFind the equation of the circle which passes through the origin and cuts off chords of lengths 4 and 6 on the positive side of the x-axis and y-axis respectively.
View SolutionFind the locus of the centre of a circle which passes through the origin and cuts off a length 2l from the line x=c.
View SolutionFind the equation of the circle which passes through the origin and cuts off intercepts 6 and 8 from the positive parts of xandy axes respectively.
View SolutionFind the equation of the circle which passes through the origin and cuts off intercepts 3and4 from the positive parts of the axes respectively.
View Solution
