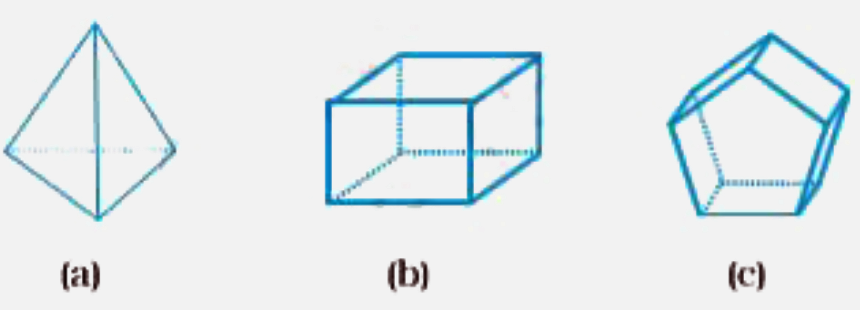
Verify Euler’s formula for these solids.
The correct Answer is:Eulers formula
Face + Vertices - Edges = 2
(1)Face=7
Vertices=10
Edges=15
Eulers = F+V−E=7+10−15=2
(2) Face=9
Vertices=9
Edges=16
Eulers = F+V−E=9+9−16=2.
To verify Euler’s formula for the given solids, we will follow these steps:
Step 1: Understand Euler's Formula
Euler's formula states that for any convex polyhedron, the relationship between the number of faces (F), vertices (V), and edges (E) is given by:
F+V−E=2
Step 2: Identify the First Solid
Let’s analyze the first solid.
Step 2.1: Count the Faces (F)
- The first solid has 7 faces.
Step 2.2: Count the Vertices (V)
- The solid has 10 vertices (5 on the top face and 5 on the base).
Step 2.3: Count the Edges (E)
- The solid has 15 edges (5 edges on the top face, 5 edges on the base, and 5 edges connecting the top to the base).
Step 3: Apply Euler's Formula for the First Solid
Now, we will substitute the values into Euler's formula:
F+V−E=7+10−15
Calculating this gives:
17−15=2
Step 4: Verify for the First Solid
Since the result is equal to 2, we have verified Euler's formula for the first solid.
Step 5: Identify the Second Solid
Now, let’s analyze the second solid.
Step 5.1: Count the Faces (F)
- The second solid has 9 faces (4 triangular faces and 1 base face).
Step 5.2: Count the Vertices (V)
- The second solid has 9 vertices.
Step 5.3: Count the Edges (E)
- The second solid has 16 edges.
Step 6: Apply Euler's Formula for the Second Solid
Now, we will substitute the values into Euler's formula:
F+V−E=9+9−16
Calculating this gives:
18−16=2
Step 7: Verify for the Second Solid
Since the result is equal to 2, we have verified Euler's formula for the second solid as well.
Conclusion
Both solids satisfy Euler's formula, confirming that F+V−E=2 holds true for both cases.
---
Euler's formula states that for any convex polyhedron, the relationship between the number of faces (F), vertices (V), and edges (E) is given by:
F+V−E=2
Let’s analyze the first solid.
- The first solid has 7 faces.
- The solid has 10 vertices (5 on the top face and 5 on the base).
- The solid has 15 edges (5 edges on the top face, 5 edges on the base, and 5 edges connecting the top to the base).
Now, we will substitute the values into Euler's formula:
F+V−E=7+10−15
Calculating this gives:
17−15=2
Since the result is equal to 2, we have verified Euler's formula for the first solid.
Now, let’s analyze the second solid.
- The second solid has 9 faces (4 triangular faces and 1 base face).
- The second solid has 9 vertices.
- The second solid has 16 edges.
Now, we will substitute the values into Euler's formula:
F+V−E=9+9−16
Calculating this gives:
18−16=2
Since the result is equal to 2, we have verified Euler's formula for the second solid as well.
Both solids satisfy Euler's formula, confirming that F+V−E=2 holds true for both cases.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A binary solid(A+B−) has a zinc blende stracture with B ions constituting the lattice and A+ inos occupying 25% of the terahedral holes. The formula of the solid is
AABBA2BCAB2DAB4A binary solid (A+B−) has a zinc blende structure with B− ions constituting the lattice and A+ ions occupying 25% tetrahedral holes. The formula of the solid is
AAB2BABCA2BDAB4A binary solid A+B− has a structure with B− ions constituting the lattice and A+ ions occupying 25% tetrahedral holes. Formula of the solid is
AA2BBABCAB2DAB4
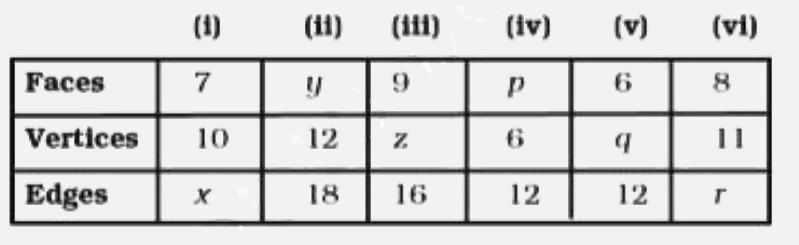
Complete the following table and verify Euler’s formula in each case.
View SolutionUsing Euler’s formula, find the value of unknown x, y, z, p, q, r, in the following table.
View SolutionEuler’s formula is true for all three-dimensional shapes.
View SolutionUsing Euler’s formula find the unknown.
Faces ?,5,20 ,
vectices 6,?,12
Edges 12,9,?
View SolutionIf the ratio of co-ordination no P to that of Q be Y:Z , then the formula of the solid is
View Solution