Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
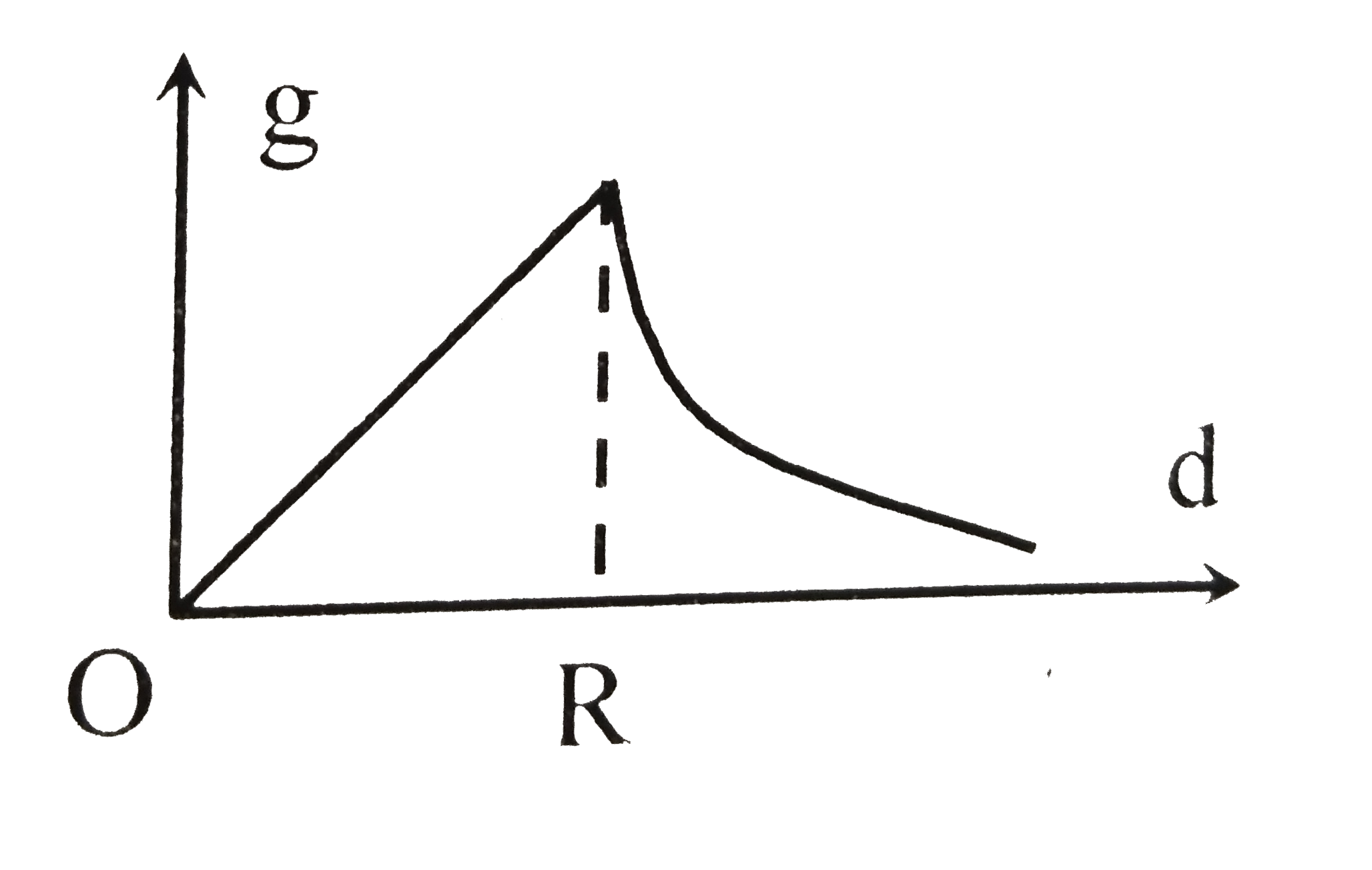
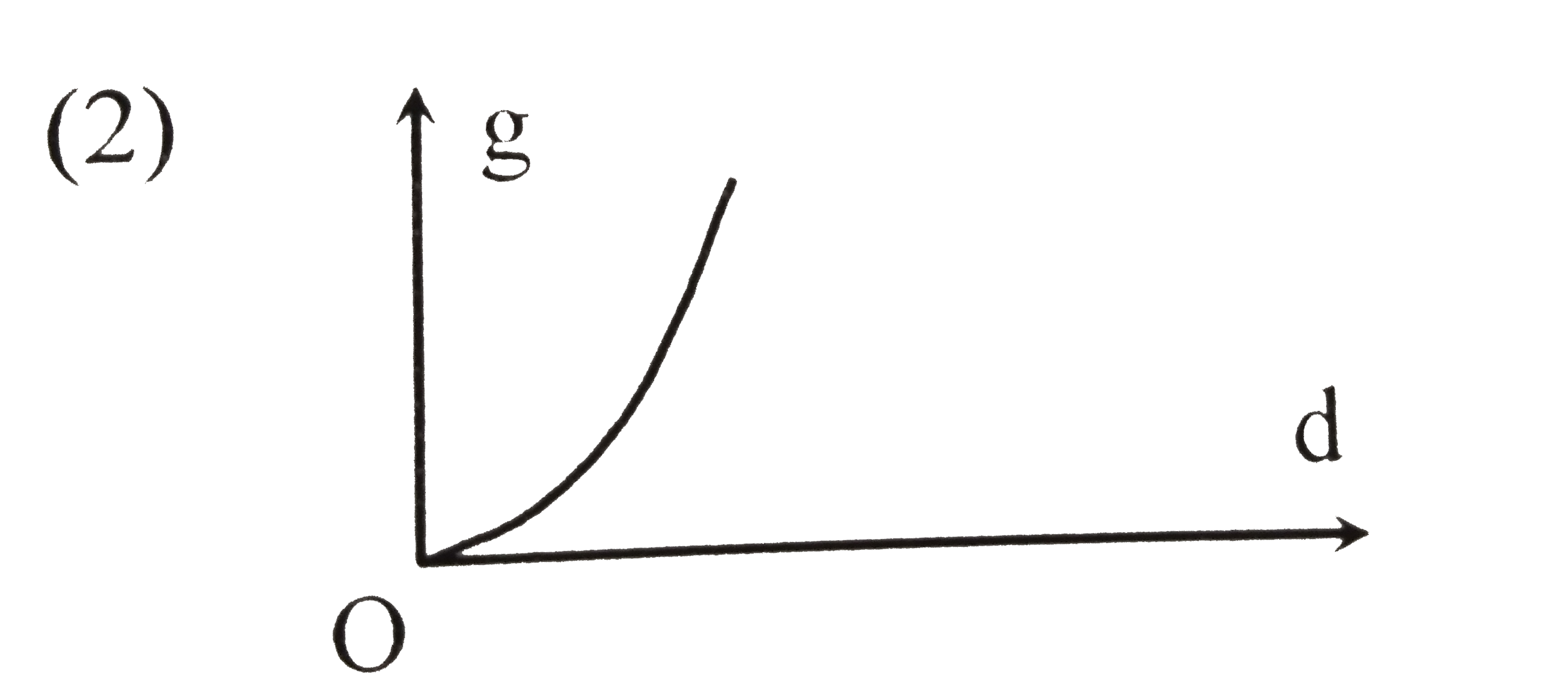
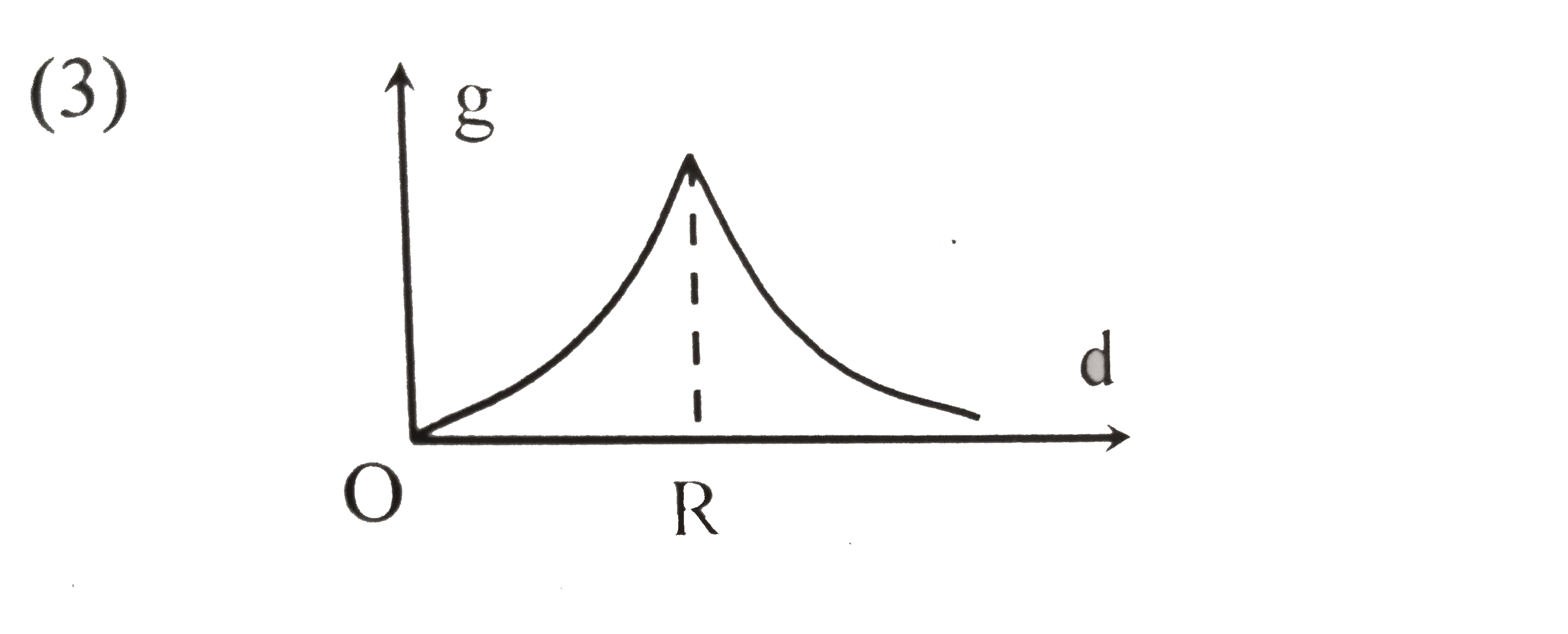
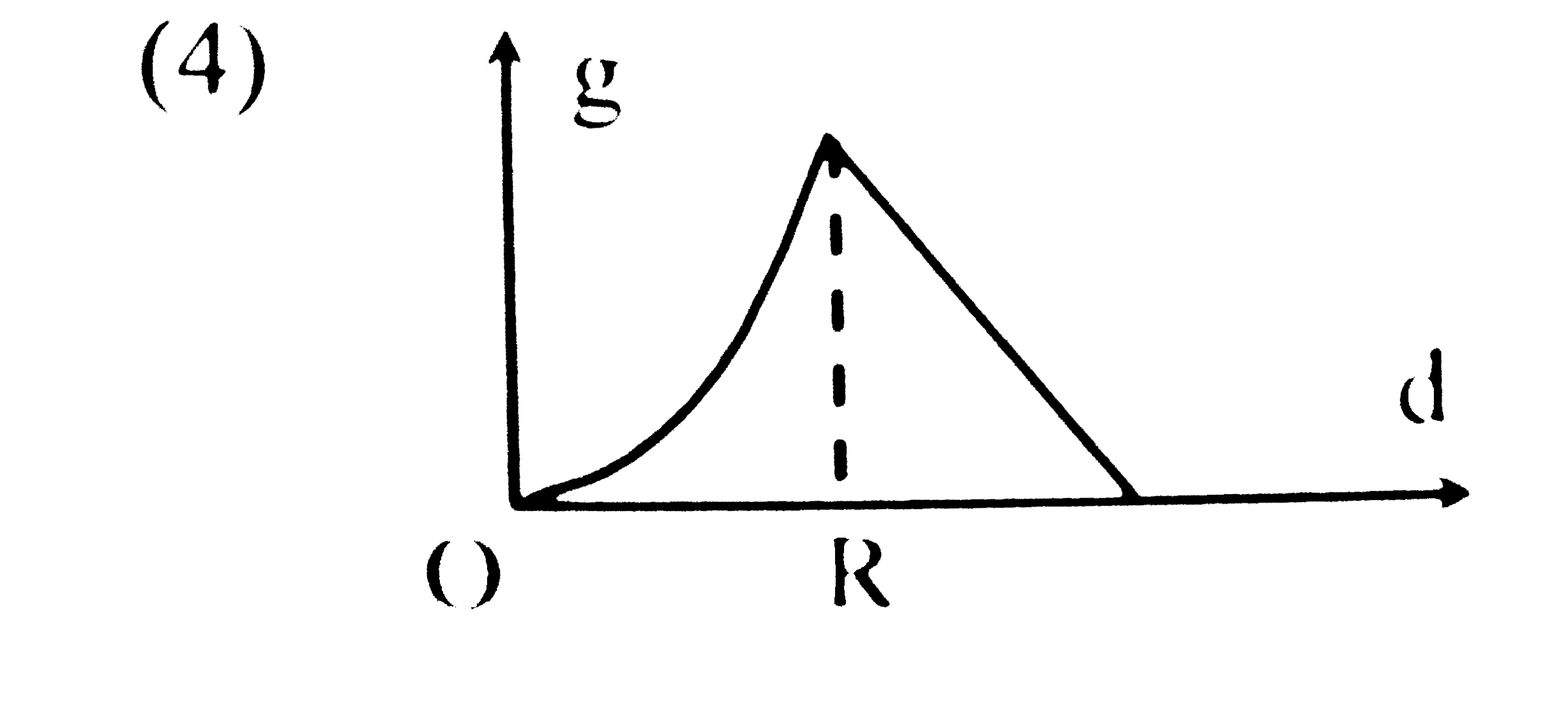
The correct Answer is:A
Step by step video, text & image solution for Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
AR/2B√2RCR√2D(√2−1)R - Question 2 - Select One
At the centre of earth the acceleration due to gravity is
AinfiniteBzeroC9.8ms−2Dall of these - Question 3 - Select One
One goes from the centre of the earth to a distance two third the radius of the earth. The acceleration due to gravity is highest at
Athe centre of the earthBa distance half the radius of the earthCa distance one-third of the radius of the earthDa distance two-third of the radius of the earth
Starting from the surface of earth, the variation of acceleration due to gravity (g) with height (h) can be represented by
View SolutionObtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.
View SolutionIf g is acceleration due to gravity on the surface of the earth,having radius R ,the height at which the acceleration due to gravity reduces to g/2 is
View SolutionDoes the concentration of the earth's mass near its centre change the variation of g (acceleration due to gravity) with height from its surface?
View SolutionAt what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
View Solution

