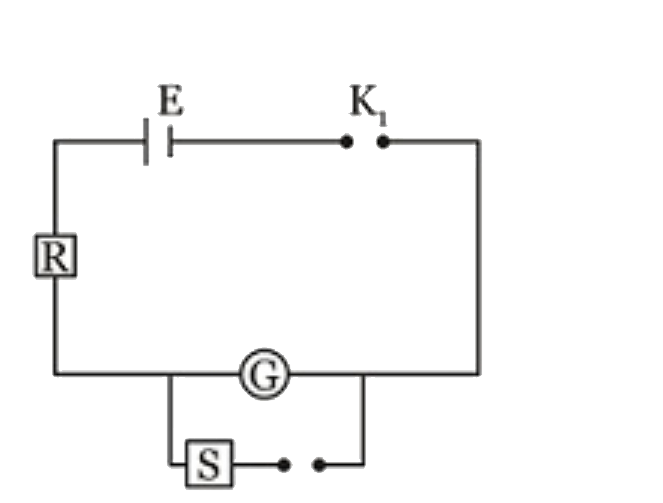
In a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 kΩ are used. The figure of merit of the galvanometer is 60 μA/division. In the absence of shunt resistance, the galvanometer produces a deflection of θ=9 divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of θ/2, is closet to :
A
550Ω
B
220Ω
C
55Ω
D
110Ω
Video Solution
Text Solution
The correct Answer is:D
|
Answer
Step by step video, text & image solution for In a circuit for finding the resistance of a galvanometer by half deflection method, a 6 V battery and a high resistance of 11 kOmega are used. The figure of merit of the galvanometer is 60 muA//"division". In the absence of shunt resistance, the galvanometer produces a deflection of theta =9 divisions when current flows in the circuit. The value of the shunt resistance that can cause the deflection of theta//2, is closet to : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
Similar Practice Problems
- Question 1 - Select One
The deflection in a galvanometer decreases to 1/5th of the original deflectioon, if it is shunted by a resistance of 5Ω. The resistance of the galvanometer is
A1ΩB10ΩC15ΩD20Ω - Question 1 - Select One
To know the resistance of a galvanometer by half deflection method, a battery of emf V and resistance R is used to deflect the galvanometer by angle θ . If a shunt of resistance is needed to get half deflection then, G, R and S are related by the equation :
A2S(R+G)=RGBS(R+G)=RGC2S=GD2G=S - Question 1 - Select One
To know the resistance G of a galvanometer by half deflection method , a battery of emf VE and resistance R is used to deflect the galvanometer by angle θ . If a shunt of resistance S is needed to get half deflection then , G,R and S related by the equation :
A2S(R+G)=RGBS(R+G)=RGC2S=GD2G=S - Question 1 - Select One
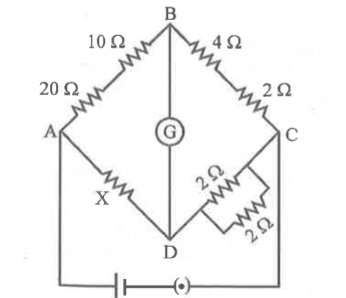
In an experiment to determine the resistance of a galvanometer by half deflection method, the circuit shown is used. In one set of readings , if R=10ΩS=4Ω, then the resistance of the galvanometer is
 A203ΩB403ΩC503ΩD703Ω
A203ΩB403ΩC503ΩD703Ω - Question 1 - Select One
When a moving coil galvanometer is shunted with a resistance of 10Ω,the deflection in the galvanometer reduces from 30 divisions to 6 divisions. The resistance of the galvanometer is
A40ΩB50ΩC30ΩD20Ω - Question 1 - Select One
The deflection of a moving coil galvanometer reduces to half on shunting it with a resistance of 60Ω . The resistance of galvanometer is
A30ΩB120ΩC60ΩD15Ω - Question 1 - Select One
The deflection in a moving coil galvanometer falls from 100 divisions to 20 divitation when a shunt of 12Ω is used. The resistance of the galvanometer coilds is
A3ΩB12ΩC48ΩD48/5Ω - Question 1 - Select One
A moving coil galvanometer of resistance 100Ω is used as an ammeter using a resistance 0.1Ω. The maximum diflection current in the galvanometer is 100μA. Find the minimum current in the circuit so that the ammeter shows maximum deflection
A100.1 mAB1000.1 mAC10.01 mAD1.01 mA