You move a ball of mass m away form a sphere of mass M. (a) Does the gravitational patential energy of the systemof ball and sphere increase or decrease ? (b) Is positive work or negative work done by the gravitational force between the ball and the sphere ?
To solve the problem step by step, we will analyze the gravitational potential energy and the work done by the gravitational force when moving a ball of mass m away from a sphere of mass M.
Step 1: Understanding Gravitational Potential Energy
The gravitational potential energy U between two masses m and M separated by a distance r is given by the formula:
U=−GmMr
where G is the gravitational constant.
Step 2: Analyzing the Change in Potential Energy
As the ball is moved away from the sphere, the distance r increases. When r increases, the value of U becomes less negative (i.e., it approaches zero).
- At r=R (the surface of the sphere), U=−GmMR.
- As r approaches infinity, U approaches 0.
Since moving from a more negative value to a less negative value indicates an increase in potential energy, we conclude:
Gravitational potential energy increases.
Step 3: Determining the Work Done by Gravitational Force
The work done W by the gravitational force when moving the ball away can be calculated using the formula:
W=F⋅d⋅cos(θ)
where F is the gravitational force, d is the displacement, and θ is the angle between the force and displacement vectors.
Step 4: Direction of Forces and Displacement
- The gravitational force F acts towards the center of the sphere (attraction).
- The displacement d is away from the sphere.
Since the angle θ between the gravitational force and the displacement is 180∘:
cos(180∘)=−1
Thus, the work done is:
W=F⋅d⋅(−1)=−F⋅d
This indicates that the work done by the gravitational force is negative.
Conclusion
(a) The gravitational potential energy of the system increases as the ball is moved away from the sphere.
(b) The work done by the gravitational force between the ball and the sphere is negative.
---
The gravitational potential energy U between two masses m and M separated by a distance r is given by the formula:
U=−GmMr
where G is the gravitational constant.
As the ball is moved away from the sphere, the distance r increases. When r increases, the value of U becomes less negative (i.e., it approaches zero).
- As r approaches infinity, U approaches 0.
Gravitational potential energy increases.
The work done W by the gravitational force when moving the ball away can be calculated using the formula:
W=F⋅d⋅cos(θ)
where F is the gravitational force, d is the displacement, and θ is the angle between the force and displacement vectors.
- The gravitational force F acts towards the center of the sphere (attraction).
- The displacement d is away from the sphere.
cos(180∘)=−1
Thus, the work done is:
W=F⋅d⋅(−1)=−F⋅d
This indicates that the work done by the gravitational force is negative.
(a) The gravitational potential energy of the system increases as the ball is moved away from the sphere.
Topper's Solved these Questions
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PROBLEMS
63 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
16 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
Similar Questions
A particle of mass 1kg is kept on the surface of a uniform sphere of mass 20kg and radius 1.0m. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionkAS particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to bbe dne against the gravitational force between them to take the particle away from the sphere.
View Solution
Knowledge Check
Two spheres, each of mass 625 kg, are placed with their centres 50 cm apart. The gravitational force between them is
A10.42 dyneB15.42 dyneC20.42 dyneD5.42 dyneA ball of mass of 500 gram is projected vertically upwards with a speed of 4m/s. What is the maximum gravitational potential energy of the ball?
A2.5JB3JC3.5JD4JSTATEMENT-1: The gravitational potential energy of a solid sphere is negative.
STATEMENT-2: Two masses attract each other.AStatement-1 is True, Statement-2 is True, Statement-2 is a correct explanation, for Statement-1.BStatement-1 is True, Statement-2 is True, Statement-2 is not a correct explanation for Statement-1.CStatement-1 is True, Statement-2 is False.DStatement-1 is a False, Statement-2 is True.
A particle of mass m is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere,
(b) the gravitational force which the sphere exerts on the particle.
View SolutionA uniform ring of mass m and radius 3a is kept above a sphere of mass M and radius 3a at a distance of 4a (as shown in figure) such that line joining the centres of ring and sphere is perpendicular to the plane of the ring. Find the force of gravitational attraction between the ring and the sphere.
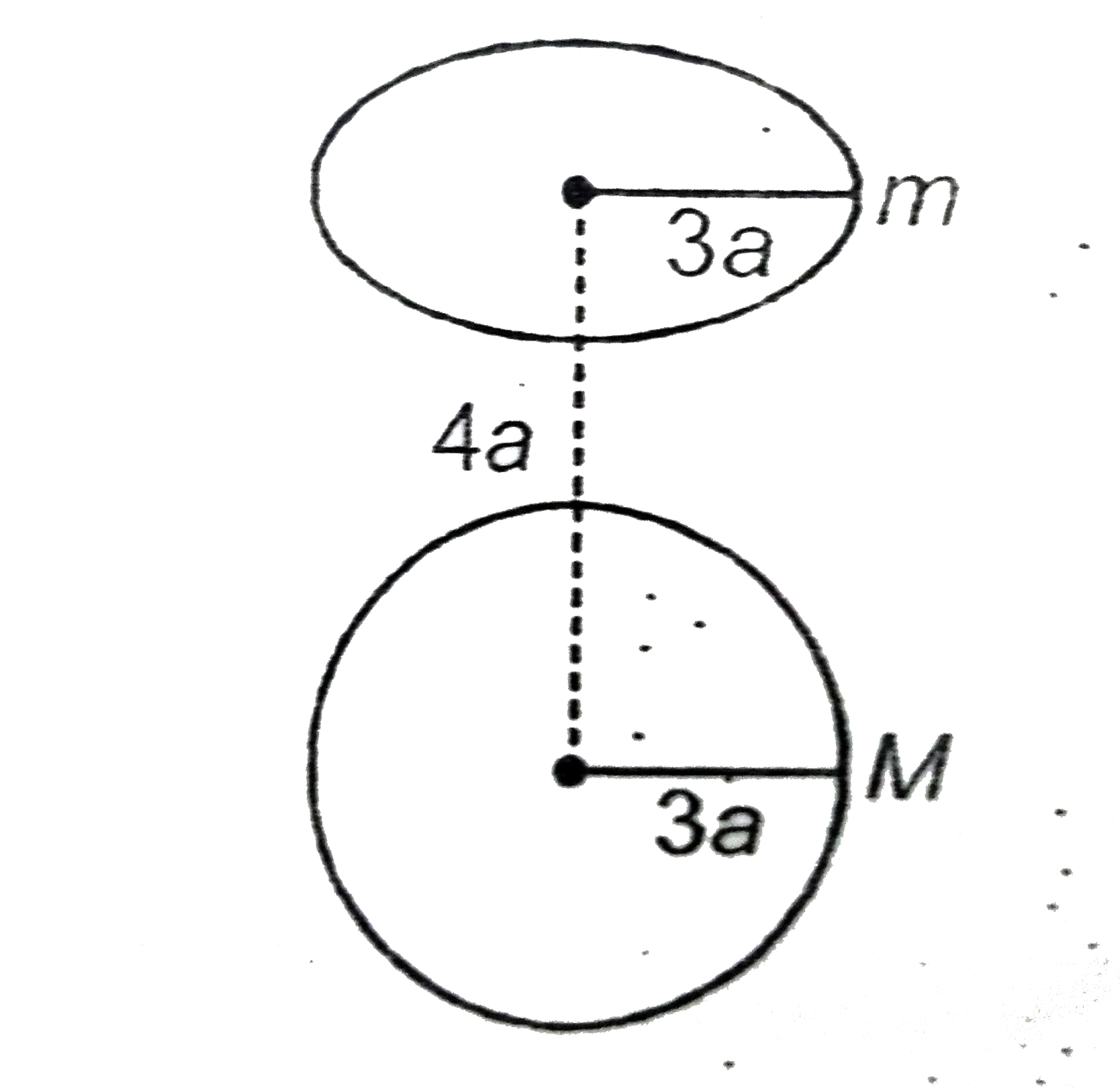
View SolutionIn the above probllem, the normal force between the ball and the shell in position B is (m=mass of ball)
View SolutionTwo spheres of masses m and M are situated in air and the gravitational force between them is F. The space around the masses is now filled with a liquid of specific gravity 3. The gravitational force will now be
View SolutionTwo sphere of masses m and M are situated in air and the gravitational force between them is F. The space around the masses in now filled with a liquid of specific gravity 3. The gravitational force will now be
View Solution
