A 68 kg crate is dragged across a floor by pulling on a rope attached to the crate and inclined 15∘ above the horizontal.
(a) If the coefficient of static friction is 0.50, what minimum force magnitude is required from the rope to start the crate moving?
(b) If μk=0.35, what is the magnitude of the initial acceleration of the crate?
To solve the problem step by step, we will break it down into parts (a) and (b) as given in the question.
Part (a): Minimum Force to Start Moving the Crate
1. Identify the Forces Acting on the Crate:
- Weight of the crate (W) = mg=68kg×g (where g≈9.8m/s2)
- Normal force (N)
- Applied force (F) at an angle of 15∘ above the horizontal
- Frictional force (f), which opposes the motion
2. Calculate the Weight of the Crate:
W=68kg×9.8m/s2=666.4N
3. Resolve the Applied Force (F):
- Horizontal component: Fx=Fcos(15∘)
- Vertical component: Fy=Fsin(15∘)
4. Determine the Normal Force (N):
Since the crate is not moving vertically, we can set up the equation for vertical forces:
N+Fy=W⟹N+Fsin(15∘)=666.4N
Thus,
N=666.4N−Fsin(15∘)
5. Calculate the Maximum Static Friction Force (f_max):
fmax=μsN=0.5×N
6. Set Up the Equation for Horizontal Forces:
At the point of impending motion, the applied horizontal force equals the maximum static friction:
Fx=fmax⟹Fcos(15∘)=0.5×N
7. Substituting N into the Friction Equation:
Substitute N from step 4 into the friction equation:
Fcos(15∘)=0.5(666.4N−Fsin(15∘))
8. Rearranging the Equation:
Fcos(15∘)+0.5Fsin(15∘)=0.5×666.4N
F(cos(15∘)+0.5sin(15∘))=333.2N
9. Solving for F:
F=333.2Ncos(15∘)+0.5sin(15∘)
Calculate the values using cos(15∘)≈0.9659 and sin(15∘)≈0.2588:
F≈333.20.9659+0.5×0.2588≈300N
Part (b): Magnitude of Initial Acceleration of the Crate
1. Identify the Kinetic Friction:
The coefficient of kinetic friction μk=0.35.
2. Calculate the Normal Force (N):
Using the previously derived expression for N:
N=666.4N−300sin(15∘)
Calculate 300sin(15∘):
300sin(15∘)≈300×0.2588≈77.64N
Thus,
N≈666.4−77.64≈588.76N
3. Calculate the Kinetic Friction Force (f_k):
fk=μkN=0.35×588.76≈206.06N
4. Set Up the Net Force Equation:
The net force acting on the crate when it is moving:
Fnet=Fcos(15∘)−fk
Substitute F=300N:
Fnet=300cos(15∘)−206.06
Calculate 300cos(15∘):
300cos(15∘)≈300×0.9659≈289.77N
Thus,
Fnet≈289.77−206.06≈83.71N
5. Calculate the Acceleration (a):
Using Newton's second law:
a=Fnetm=83.7168≈1.23m/s2
Final Answers:
(a) The minimum force required to start moving the crate is approximately 300 N.
(b) The magnitude of the initial acceleration of the crate is approximately 1.23 m/s².
- Weight of the crate (W) = mg=68kg×g (where g≈9.8m/s2)
- Normal force (N)
- Applied force (F) at an angle of 15∘ above the horizontal
- Frictional force (f), which opposes the motion
W=68kg×9.8m/s2=666.4N
- Horizontal component: Fx=Fcos(15∘)
- Vertical component: Fy=Fsin(15∘)
Since the crate is not moving vertically, we can set up the equation for vertical forces:
N+Fy=W⟹N+Fsin(15∘)=666.4N
Thus,
N=666.4N−Fsin(15∘)
fmax=μsN=0.5×N
At the point of impending motion, the applied horizontal force equals the maximum static friction:
Fx=fmax⟹Fcos(15∘)=0.5×N
Substitute N from step 4 into the friction equation:
Fcos(15∘)=0.5(666.4N−Fsin(15∘))
Fcos(15∘)+0.5Fsin(15∘)=0.5×666.4N
F(cos(15∘)+0.5sin(15∘))=333.2N
F=333.2Ncos(15∘)+0.5sin(15∘)
Calculate the values using cos(15∘)≈0.9659 and sin(15∘)≈0.2588:
F≈333.20.9659+0.5×0.2588≈300N
The coefficient of kinetic friction μk=0.35.
Using the previously derived expression for N:
N=666.4N−300sin(15∘)
Calculate 300sin(15∘):
300sin(15∘)≈300×0.2588≈77.64N
Thus,
N≈666.4−77.64≈588.76N
fk=μkN=0.35×588.76≈206.06N
The net force acting on the crate when it is moving:
Fnet=Fcos(15∘)−fk
Substitute F=300N:
Fnet=300cos(15∘)−206.06
Calculate 300cos(15∘):
300cos(15∘)≈300×0.9659≈289.77N
Thus,
Fnet≈289.77−206.06≈83.71N
Using Newton's second law:
a=Fnetm=83.7168≈1.23m/s2
(a) The minimum force required to start moving the crate is approximately 300 N.
(b) The magnitude of the initial acceleration of the crate is approximately 1.23 m/s².
Topper's Solved these Questions
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - CHECKPOINTS
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PROBLEMS
33 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GAUSS' LAW BOOK - RESNICK AND HALLIDAYCHAPTER - GAUSS' LAW EXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
3 Videos
Similar Questions
In Fig. 6-48, a 2.0 kg block lies on a 20 kg trolley that can roll across a floor on frictionless bearings. Between the block and the trolley, the coefficient of kinetic friction is 0.20 and the coefficient of static friction is 0.25. When a horizontal 2.0 N force is applied to the block, what are the magnitudes of (a) the frictional force between the block and the trolley and (b) the acceleration of the trolley?

View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
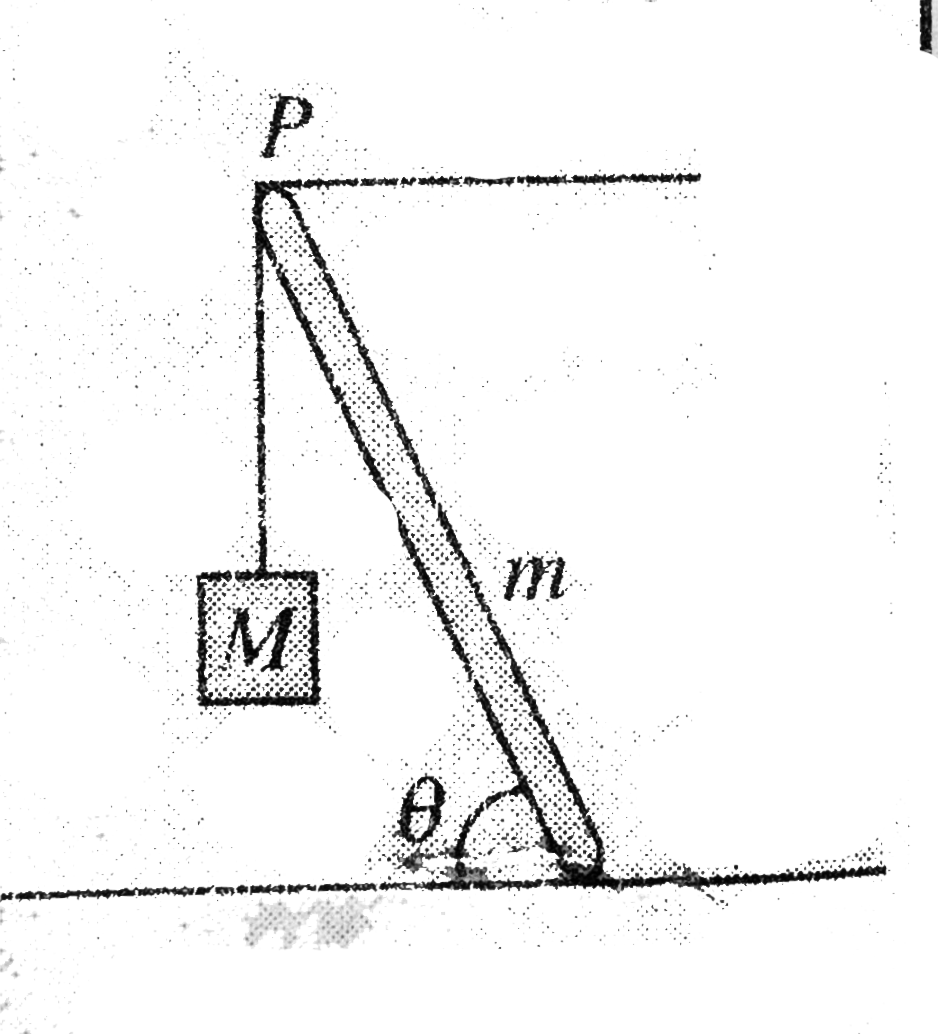 .
.
View Solution
Knowledge Check
A man drags an m kg crate across a floor by pulling on a rope inclined at angle θ above the horizontal. If the coefficient of static friction between the floor and crate is then the tension required in the rope to start the crate moving is :
Aμsmg(sinθ−μscosθ)Bμsmg(sinθ+μscosθ)Cμsmg(cosθ−μssinθ)Dμsmg(cosθ+μssinθ)A body of mass 10 kg is lying on a rough plane inclined at an angle of 30∘ to the horizontal and the coefficient of friction is 0.5. the minimum force required to pull the body up the plane is
A914 NB91.4 NC9.14 ND0.914 NA block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 N
Two forces are applied to a 5.0 kg crate, one is 6.0N to the north and the other is 8.0N to the west. The magnitude of the acceleration of the crate is :
View SolutionA 1.00×102 kg crate is being pushed across a horizontal floor by a force →P that makes an angle of 30.0∘ below the horizontal. The coefficient of kinetic friction is 0.200. What should be the magnitude of →P, so that the net work done by it and the kinetic frictional force is zero ?
View SolutionA forward horizontal force of 12 N is used to pull a 240 N crate at constant velocity across a horizontal floor. The coefficient of friction is
View SolutionA 225 kg crate rests on a surface that is inclined above the horizontal at an angle of 20.0∘.A horizontal force (magnitude = 535 N and parallel to the ground, not the incline) is required to start the crate moving down the incline. What is the coefficient of static friction between the crate and the incline?
View SolutionA blocky of mass m rests on a horizotal floor with which it has a coefficient of static friction μ. It is desired to make the body move by applying the minimum possible force F. Find the magnitude of F and the direction in which it has be applies.
View Solution
