Let $ˆ u = u_{1} ˆ i + u_{2} ˆ j + u_{3} ˆ k$ be a unit vector in be a unit vector in $R^{3} and ˆ w = \frac{1}{\sqrt{6}} (ˆ i + ˆ j + 2 ˆ k)$ .Given that there exists vector $ˆ v$ in $R^{3}$ such that $| ˆ u \times \to v | = 1 and ˆ w . (ˆ u \times \to v) = 1$ . Which of the following statement(s) is(are) correct?

A

There is exactly one choice for such V

B

There are infinitely many choice for such v

C

if $ˆ u$ lines in the XY- plane then $| u_{1} | = | u_{2} |$

D

If $ˆ u$ lies in the XY- plane then $2 | u_{1} | = | u_{2} |$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C

Let 0 be the angle between $ˆ u and \to v$
$∴ | U \times \to v | = 1 \Rightarrow | u | \to v ∣ sin 0 = 1$
$∴ | \to v | sin 0 = 1$

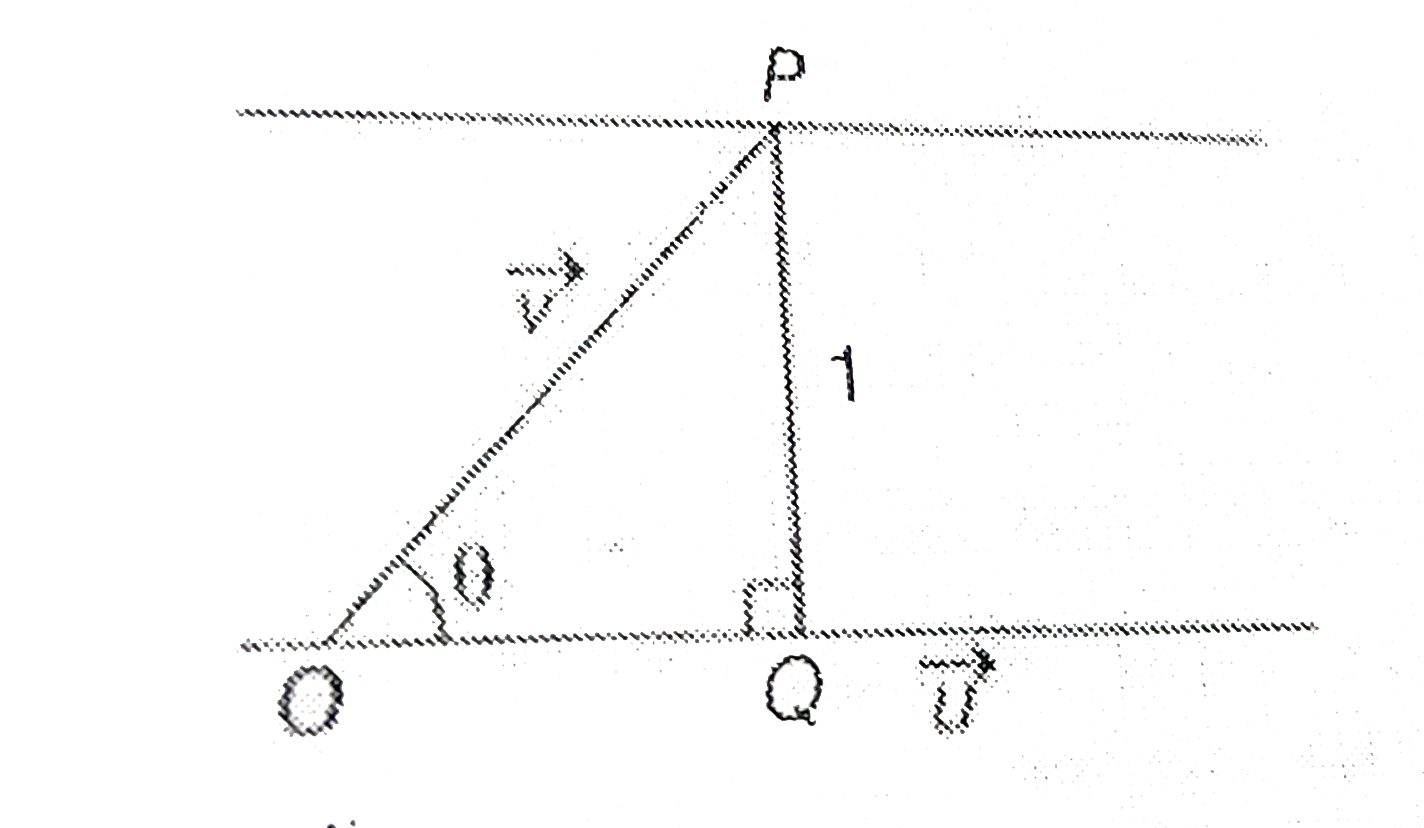
Clearly there may be infinite vectors $- - \to O P = \to v$ such that P is always 1 unit distance from $ˆ u$
$∴$ Option (b) is correct .
Again let $ϕ$ be the angle between w w and $u \times \to v .$
$∴ w . (- -- \to u \times \to v = 1 \Rightarrow | w | | u \times \to v | cos ϕ = 1$
$\Rightarrow cos ϕ = 1 \Rightarrow ϕ = 0$
Thus $w = u \times \to v$
Now if $ˆ u$ lines in XY-plane then
$u \times \to v = ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & j u_{1} & u_{2} & 0 v_{1} & v_{2} & v_{3} \end{matrix} ∣ ∣ ∣ ∣ ∣ or u = u ˆ i + u_{2} ˆ j$
$∴ w = (u_{2} v_{3}) ˆ i - (u_{1} v_{3}) ˆ j + (u_{1} u_{2} - v_{1} u_{2}) ˆ k$
$= \frac{1}{\sqrt{6}} (ˆ i + ˆ j + 2 ˆ k)$
$∴ u_{2} v_{3} = \frac{1}{\sqrt{6}}, u_{1} u_{3} = \frac{- 1}{\sqrt{6}}$
$\Rightarrow \frac{u_{2} u_{3}}{u_{1} u_{3}} = - 1 or | u_{1} | = | u_{2} |$
$∴$ Option (c ) is correct
Now if $ˆ u$ lies in XZ-plane then $u = u_{1} ˆ i + u_{3} ˆ k$
$∴ u \times \to v = ∣ ∣ ∣ ∣ ∣ \begin{matrix} ˆ i & ˆ j & ˆ k u_{1} & 0 & u_{3} v_{1} & v_{2} & v_{3} \end{matrix} ∣ ∣ ∣ ∣ ∣$
$\Rightarrow w = (- v_{2} u_{3}) ˆ i - (u_{1} v_{3} - u_{3} v_{1}) ˆ j + (u_{1} v_{2}) ˆ k$
$\Rightarrow ˆ k = \frac{1}{\sqrt{6}} (ˆ i + ˆ j + 2 ˆ k)$
$\Rightarrow - v_{2} u_{3} = \frac{1}{\sqrt{6}} and u_{1} v_{2} = \frac{2}{\sqrt{6}}$
$∴ | u_{2} | = 2 | u_{3} |$
$∴$ Option (d) is wrong

Updated on:21/07/2023

|

Class 12 MATHS VECTOR ALGEBRA

Similar Questions

Knowledge Check

The unit vector perpendicular to $\to A = 2 ˆ i + 3 ˆ j + ˆ k$ and $\to B = ˆ i - ˆ j + ˆ k$ is
A $\frac{4 ˆ i - ˆ j - 5 ˆ k}{\sqrt{42}}$
B $\frac{4 ˆ i - ˆ j + 5 ˆ k}{\sqrt{42}}$
C $\frac{4 ˆ i + ˆ j + 5 ˆ k}{\sqrt{42}}$
D $\frac{4 ˆ i + ˆ j - 5 ˆ k}{\sqrt{42}}$
Figure 2 (EP). 13 shows the orientatione of two vectors $\to u$ and $\to v$ in the (XY) plane.
If $\to u = a ˆ I + b ˆ j$ and $\to v = p ˆ + q ˆ j$ which of the following is correct ?
.
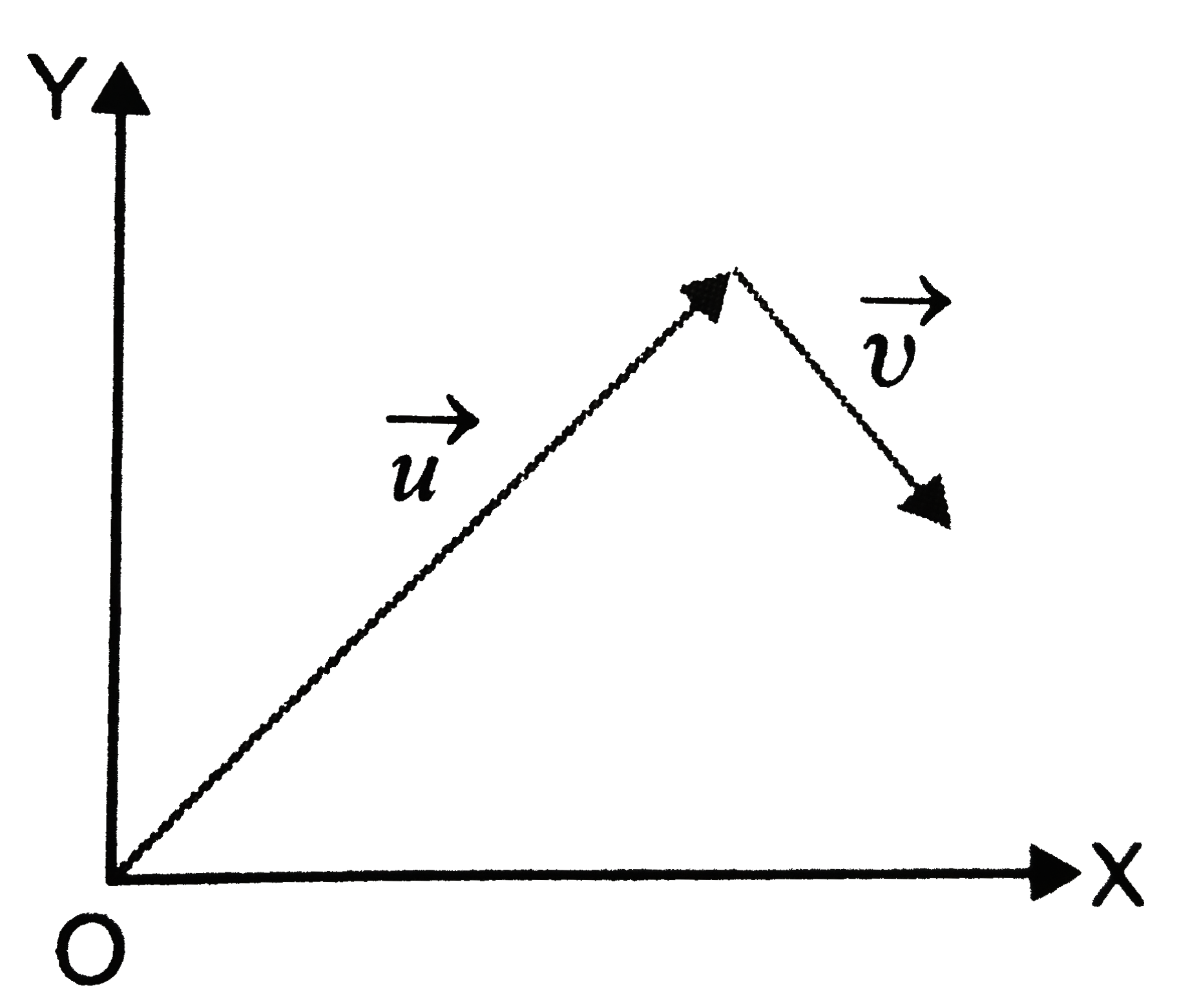A(a) $a$ and $p$ are psoitive while $b$ and $q$ are negative
B(b) $a, q$ and $b$ are positve while $q$ is negative
C(c ) $a, b, q$ and $b$ positve whicl $p$ is negative
D(d) $a, b, p$ and $q$ are all positive

Recommended Questions

Home
Ask Doubt
Profile