Question

Let $f:[0,4\pi ]\to [0,\pi ]$ be defined by $f\left(x\right)={\cos }^{-1}\left(\cos x\right).$ The number of points $x\in [0,4\pi ]$ 4satisfying the equation $f\left(x\right)=\frac{10-x}{10}$ is

Answer

3

Explanation

(i) Using definition of ` f (x) = cos ^(-1)(x)`, we trace the curve ` f(x) = cos ^(-1) ( cos x ) `.
(ii) The number of solutions of equations involving tigonometric an algebric functions and involving both functions are found using graphs of the curves.
We know that`, cos ^(-1) ( cos x ) = {{:(x",",, if x in [0"," pi]), (2 pi - x ",",, if x in [ pi"," 2pi]), (- 2pi + x ",",, if in [ 2pi"," 3pi]), ( 4pi - x ",",, if x in [ 3pi "," 4pi]):}`

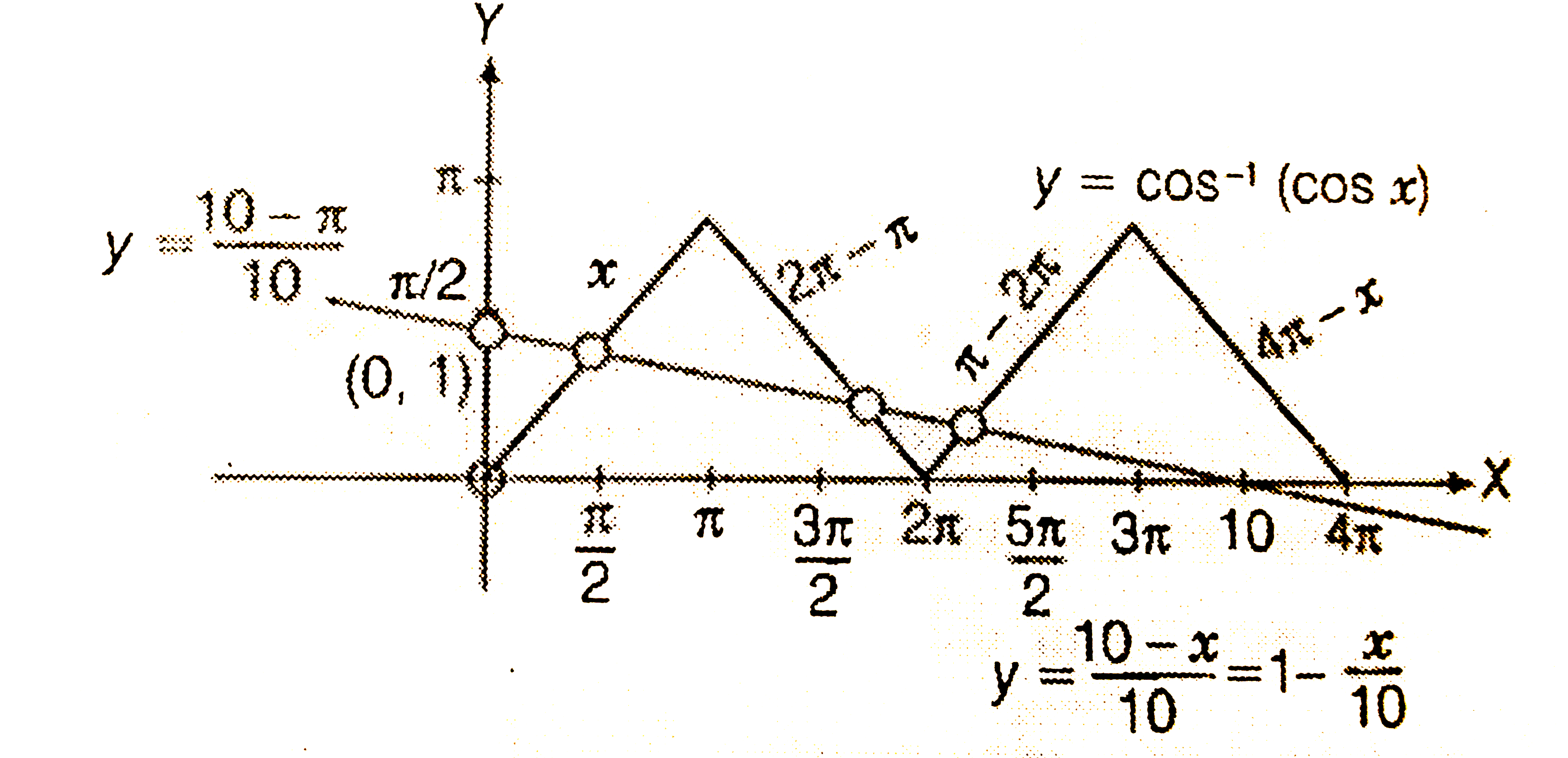
From above graph, it is clear that `y = (10 - x)/(10) and y = cos ^(-1) ( cos x)` intersect at three distinct points, so number of solutions is 3.