A company makes two kinds of leather belts, A and B. Belt A is high quality belt, and B is of lower quality. The respective profits are Rs. 40 and Rs. 30 per belt. Each belt of type A requires twice as much time as a belt of type B, and if all belts were of type B, the company could make 1000 belts per day. The supply of leather is sufficient for only 800 belts per day (both A and B combined). Belt A requires a fancy buckle, and only 400 buckles per day are available. There are only 700 buckles available for belt B. What should be the daily production of each type f belt? Formulate the problem as a LPP.
Let x belts of type A and y belts of type B be made. Then x≥0m,y≥0,x≤400,y≤700andx+y≤800.
Now, 1000 belts of type B can be made in 1 day.
∴ 500 belts of type A can be made in 1 day.
∴ time taken to make x belts of type A and y belts of type B =(x500+y1000)days.
∴x500+y1000≤1,i.e.,2x+y≤1000.
We have to maximize Z=4x+3y, subject to the constraints x≥0,y≥0,x≤400,y≤700,x+y≤800and2x+y≤1000.
We draw the graphs of the lines
x=0,y=0,x=400,y=700,x+y=800,2x+y=1000 as shown below.
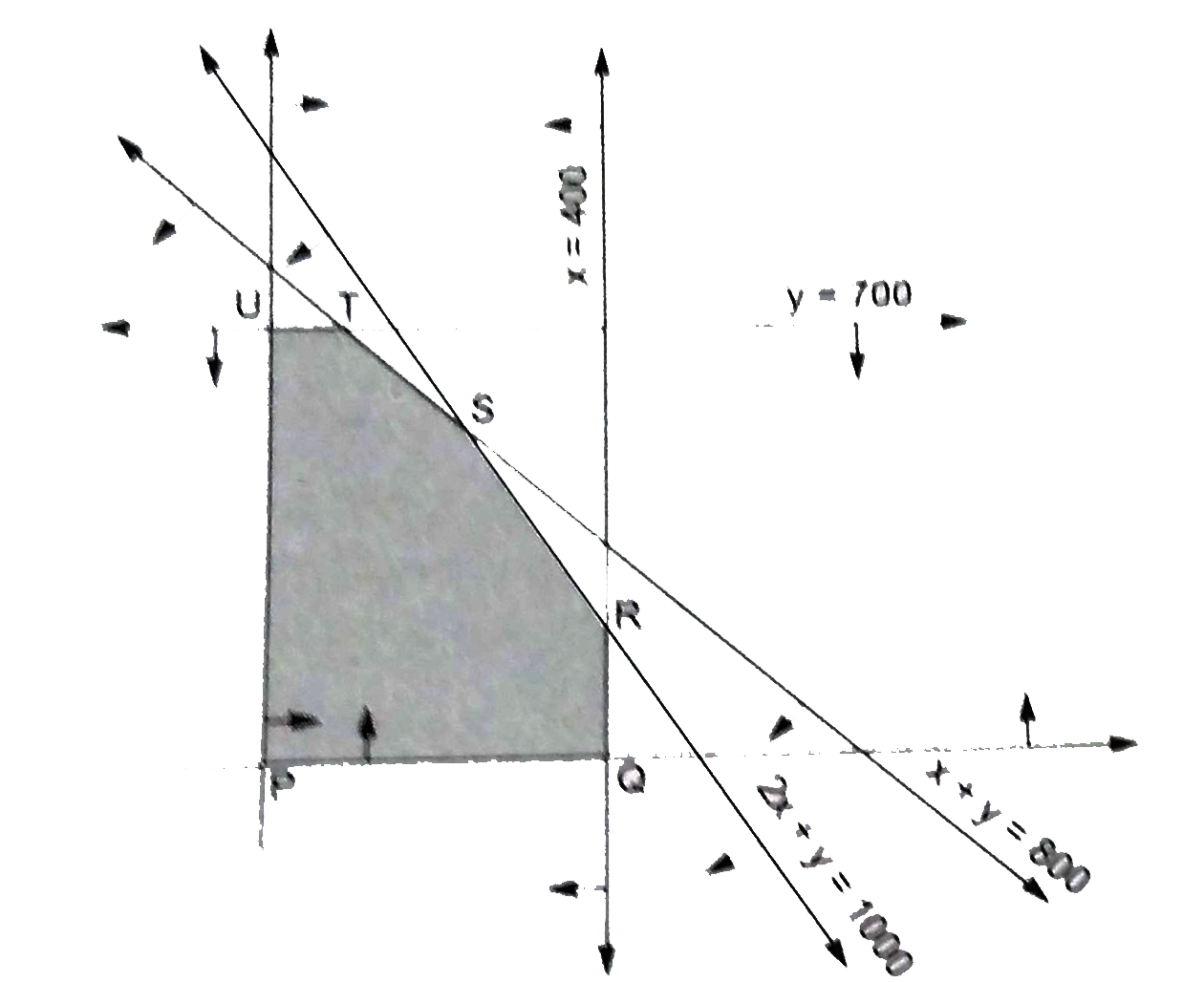
Since (0,0) satisfies x≤400, line x=400 together with the region containing O(0,0) represents x≤400.
Since (0,0) satisfies y≤700,
Since (0,0) satisfies x+y≤800, the line x+y=800 together with the region containing O(0,0) represents 2x+y≤1000.
The y-axis and the region to its right-hand side represents x≥0.
The x-axis and the region above it represents y≥0.
Thus, hte shaded region represents the feasible region, whose vertices are P, Q, R, S, T and U.
Clearly, the coordinates of P and Q are (0,0) and (400,0) respectively.
On solving x=400and2x+y=1000, we get fR(400,200).
On solving x+y=800and2x+y=1000, we get A(200,600).
On solving y=700andx+y=800, we get T(100,700).
On solving x=0andandy=700, we get U(0,700).
The values of Z=4x+3y at the points P, Q, R, S, T and E are respectively. 0,1600,2200,2600,2500and2100.
The maximum of these values is 2600 occurring at S(200,600).
∴ Z is maximum when x=200andy=600.
Thus, the company should make 200 belts of type A and 600 belts of type B to have a maximum profit.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33A
11 Videos
- LINEAR PROGRAMMINGBOOK - RS AGGARWALCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exprcise 33B
38 Videos
- LINEAR DIFFERENTIAL EQUATIONS BOOK - RS AGGARWALCHAPTER - LINEAR DIFFERENTIAL EQUATIONS EXERCISE - Objective Questions
27 Videos
- MATRICESBOOK - RS AGGARWALCHAPTER - MATRICESEXERCISE - Exercise 5F
21 Videos
Similar Questions
A company produces two types of leather belts A and B on which the profits are Rs. 40 and Rs. 30 per belt respectively. Each belt of type A requires twice as much time as required by a belt to type B.If all belts were of type B the company could produce 1000 belts per day. But the supply of leather is sufficient only for 800 belts per day. Belt A requires a fancy buckle and only 400 fancy buckles are available per day. For belt of type B only 700 buckles are available per day. How should the company manufacture the two types of belts in order to have maximum overall profit?
View SolutionA company produces two types of belts A and B. Profits on these belts are Rs. 2 and Rs. 1.50 per belt respectively. A belt of type A requires twice as much time as belt of type B. The company can produce at most 1000 belts of type B per day. Material for 800 belts per day is available. At most 400 buckles for belts of type A and 700 for type B are available per day. How much belts of each type should the company produce so as to maximise the profit?
View Solution
Knowledge Check
Shelter belts help in :
APreventing gullies and hence further soil loss.BChecking wind movement to protect soil cover.CRetaining soil moisture.DSlowing down the flow of water over soil.Shelter belts help in
APreventing gullies and hence further soil lossBChecking wind movement to protect soil coverCRetaining soil moistureDSlowing down the flow of water over soilShelter belt is a method of
Awater conservationBsoil formationCplantationDsoil conservation
