Find the equation of the circle with radius 5 whose centre lies on xaxis and passes through the point (2, 3).

Video Solution

Text Solution

Verified by Experts

It is given that the centre of the cricle lies on the x - axis.
So let $C (k, 0)$ be the centre of the circle.
Also, it is given that it passes through the point $P (2, 3)$ .
$∴$ radius of the circle = |CP|
$= \sqrt{{(k - 2)}^{2} + {(0 - 3)}^{2}}$
$= \sqrt{k^{2} - 4 k + 13}$
$\Rightarrow \sqrt{k^{2} - 4 k + 13} = 5 [∵$ radius = 5 units $]$
$\Rightarrow k^{2} - 4 k + 13 = 25 \Rightarrow k^{2} - 4 k - 12 = 0$
$\Rightarrow (k - 6) (k + 2) = 0 \Rightarrow k = 6 or k = - 2$
$∴$ centre of the circles is $(6, 0) or (- 2, 0)$ .
Hence, the required equation of the circle is
${(x - 6)}^{2} + {(y - 0)}^{2} = 5^{2} or {(x + 2)}^{2} + {(y - 0)}^{2} = 5^{2}$
$\Rightarrow x^{2} + y^{2} - 12 x + 11 = 0 or x^{2} + y^{2} + 4 x - 21 = 0$
Thus, there are two circles satisfying the given conditions.

Updated on:21/07/2023

|

Class 11 MATHS CIRCLES

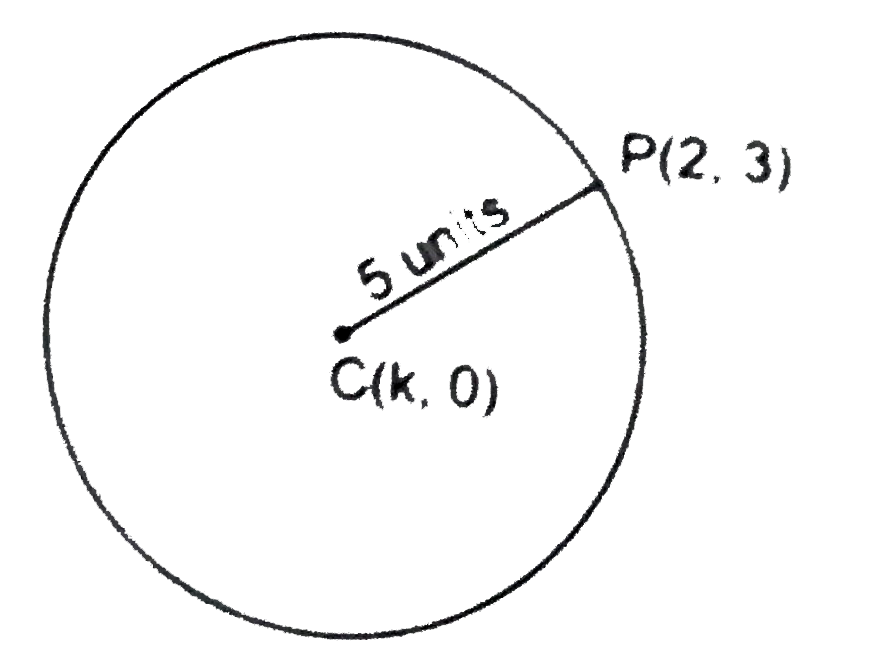
Topper's Solved these Questions

Similar Questions

Knowledge Check

The equation of the circle with radius $\sqrt{5}$ units whose centre lies. On y-axis and passes through the point (2, 3) can be
A $x^{2} + {(y - 4)}^{2} = 5$
B $x^{2} + {(y + 4)}^{2} = 5$
C ${(x - 4)}^{2} + y^{2} = 5$
D ${(x + 4)}^{2} + y^{2} = 5$

RS AGGARWAL-CIRCLE -EXERCISE 21 B

Home
Ask Doubt
Profile