The sum of an infinite geometric series is 6. If its first terms is 2, find its common ratio.
Let the infinite geometric series be a,ar,ar2,...,∞. Then,
ar=2 ...(i)
and a(1−r)=8 ...(ii)
Putting r=2a from (i) in (ii), we get
a(1−2a)=8⇒a2(a−2)=8⇒a2−8a+16=0
⇒(a−4)2=0⇒a−4=0⇒a=4.
Putting a=4 in (i), we get r=24⇒r=12.
Hence, the common ratio of the given geomwtric series is 12.
Topper's Solved these Questions
- GEOMETRICAL PROGRESSIONBOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12A
18 Videos
- GEOMETRICAL PROGRESSIONBOOK - RS AGGARWALCHAPTER - GEOMETRICAL PROGRESSIONEXERCISE - EXERCISE 12B
9 Videos
- FUNCTIONSBOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - EXERCISE 3F VERY-SHORT-ANSWER QUESTIONS
21 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - RS AGGARWALCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 19
6 Videos
Similar Questions
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
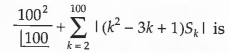 is
is
View SolutionThe sum of an infinite geometric series is 162 and the sum of its first n terms is 160. If the inverse of its common ratio is an integer, then which of the following is not a possible first term? 108 b. 144 c. 160 d. none of these
View Solution
Knowledge Check
Let Sk, be the sum of an infinite geometric series whose first term is kand common ratio is kk+1(k>0) . Then the value of ∞∑k=1(−1)kSk is equal to
A1−4loge√2Bloge2−1C1−loge2D1−loge4The H.C.F. and L.C.M. of two numbers are 12 and 336 respectively. If one of the number is 84 then the other be:
Aa. 36Bb. 48Cc. 72Dd. 96The sum of an infinite geometric series with positive terms is 3 and the sums of the cubes of its terms is 2719. Then the common ratio of this series is
A49B29C23D13
Let G Let G be the sum of infinite geometric series whose first term is sinθ and common ratio is cosθ, while G' be the sum of a different infinite geometric series whose first term cosθ and common ratio is sinθ. Find the number of solutions of the equation, G=G' in [0,2π] is
View SolutionThe sum of an infinite geometric series is 6 and the sum of its first two terms is 92 ; find its common ratio.
View SolutionThe sum of an infinite G.P. . Is 6 and its first term is 2 . Find the series
View SolutionThe sum of an infinite geometric series with positive terms is 3 and the sum of the cubes of its terms is 2719. Then, the common ratio of this series is
View SolutionThe sum of an infinite geometric progression is 6. if the sum of the first two terms is 9/2, then what is the first term ?
View Solution
