Solve:
|x+2|−xx<2,x∈R
Video Solution
Text Solution
The correct Answer is:(−∞,−2)∪(1,∞)
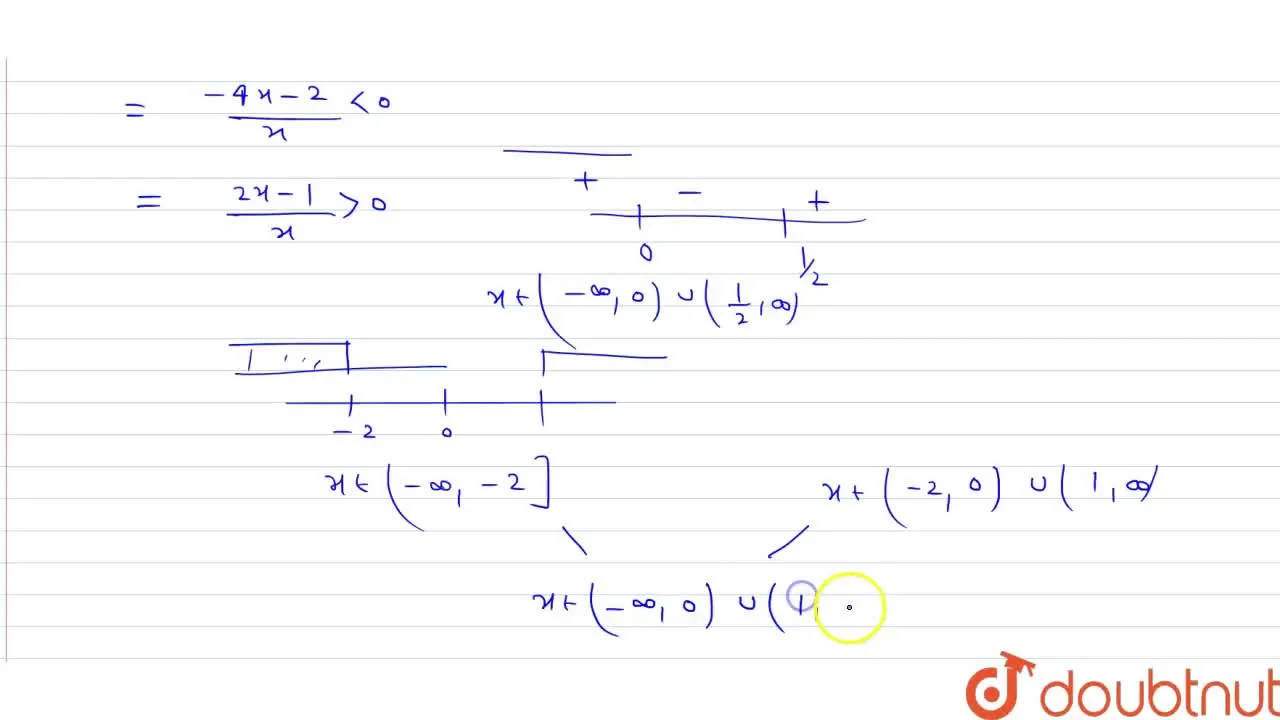
|x+2|−xx−2<0⇒|x+2|−x−2xx<0⇒|x+2|−3xx<0
Case I When x+2≥0
Then,x ge -2 and |x+2|=x+2.<br>therefore (|x+2|-3x)/(x)lt0 rArr (x+2-3x)/(x)lt0rArr(2-2x)/(x)lt0<br>rArr (2)/(x)-2lt0 rArr (2)/(x)lt2 rArr 2x lgt2 rArr x gt1.<br>therefore (xge-2 and xgt1)rArr x gt1rArrx in(1,oo).<br>CaseIIWhen x+2 lt0.<br>Then x lt -2 and |x+2| = -(x+2)<br>therefore (|x+2|-3x)/(x) lt0 rArr (-x-2-3x)/(x)lt0 rArr(-4x-2)/(x)lt0<br>rArr (4x+2)/(x)gt0 rArr 4+(2)/(x)gt0rArr (2)/(x)gt-4.<br>rArr -4xlt2 rArr x lt(-1)/(2).<br>therefore x lt-2 and x lt (-1)/(2) rArr x lt-2 rArr x in(-oo,-2).<br>Hence,solutionset=(-oo,-2)uu(1,oo).
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN ONE VARIABLE)EXERCISE - EXERCISE 6B12videos
LINEAR INEQUATIONS (IN ONE VARIABLE)
- BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN ONE VARIABLE)EXERCISE - WORD PROBLEMS (Example)9videos
LINEAR INEQUATIONS (IN ONE VARIABLE)
- BOOK - RS AGGARWALCHAPTER - LIMITEXERCISE - EXERCISE 27C15videos
LIMIT
- BOOK - RS AGGARWALCHAPTER - LINEAR INEQUATIONS (IN TWO VARIABLES )EXERCISE - EXERCISE 722videos
LINEAR INEQUATIONS (IN TWO VARIABLES )
Similar Questions
Solve : x+2x+1<0
View SolutionSolve: |x|−1|x|−2≥0,x∈R,x≠±2.
View SolutionSolve:
∣∣∣2x−1x−1∣∣∣>2,x∈RView SolutionSolve:
5x+44−x<2,x∈RView SolutionSolve:
x−3x+1<0,x∈RView SolutionSolve : |x+2|<3
View SolutionSolve 0<|x|<2
View SolutionSolve : x2+x−4x<1andx2<64
View SolutionSolve : ∣∣x2−x−6∣∣=x+2,x∈R
View SolutionThe solution set of the inequlity |x−2|−xx<2 is
View Solution