Question

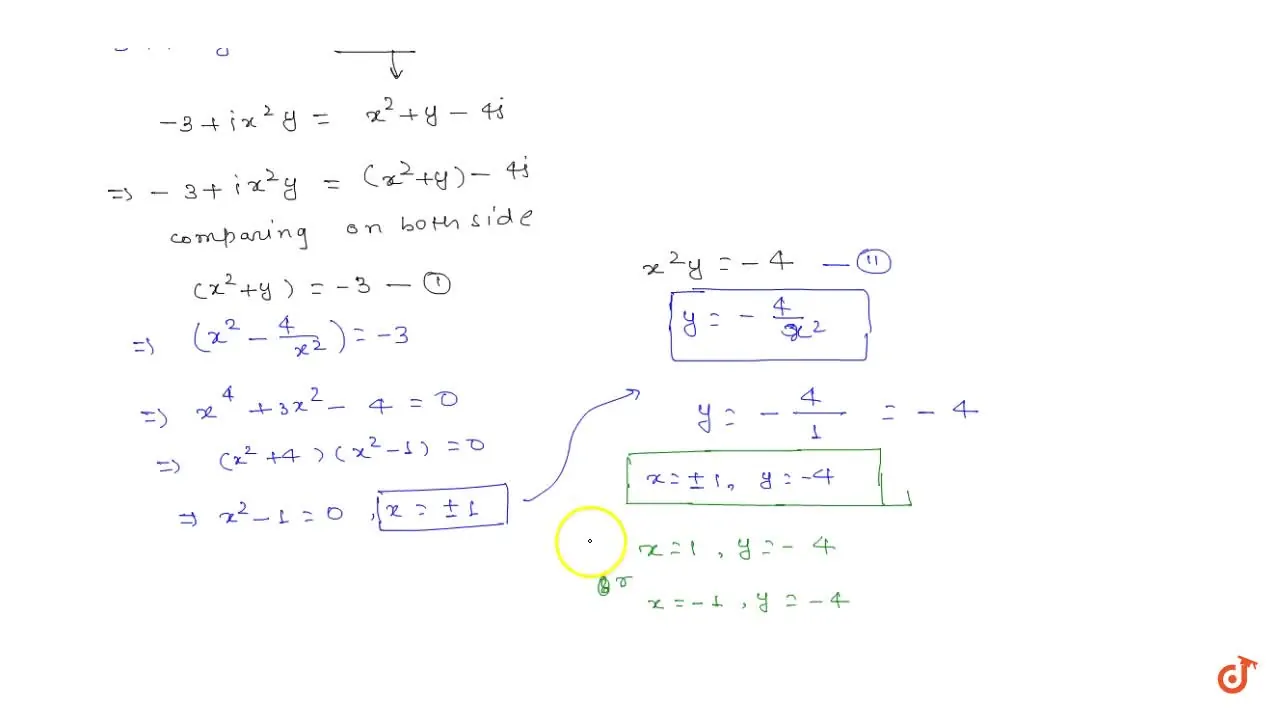
Find real values of $xandy$
for which the complex numbers $-3+i{x}^{2}yan{dx}^2+y+4i$
are conjugate of each other.

Answer

`(x =1, y = -4) or (x = -1, y = -4)`

Explanation

`(-3+iyx^(2))=(bar(x^(2)+y+4i))`
`rArr" "(-3+iyx^(2))=(x^(2)+y-4i)`
`rArr" "(x^(2)+y+3)-(4+yx^(2))i = 0`
`rArr" "x^(2)+y+3=0 and 4 + yx^(2) = 0`
`rArr" "x^(2)+y = -3" "...(i)" "and yx^(2) = -4" "...(ii)`.
Putting `x^(2) = (-3-y)` from (i) in (ii), we get
`y(-3-y) = -4 rArr y^(2)+3y - 4 = 0 rArr (y+4)(y-1)=0 rArr y = -4 or y = 1`.
Now, `y = 1 rArr x^(2) = -4 rArr x` is imaginary. So, y `in` 1.
When y = -4, we get `x^(2) = (-3+4)=1 rArr x = +- 1`.
`therefore" "(x =1, y = -4) or (x = -1, y = -4)`.