Question

In a survey of $25$ students, it was found that $12$ have taken physics, $11$ have taken chemistry and $15$ have taken mathematics; $4$ have taken physics and chemistry; $9$ have taken physics and mathematics; $5$ have taken chemistry and mathematics while $3$ have taken all the three subjects. Find the number of students who have taken (i) physics only (ii) chemistry only; (iii) mathematics only (iv) physics and chemistry but not mathematics; (v) physics and mathematics but not chemistry; (vi) only one of the subjects; (vii) at least one of the three subjects; (vii) none of the three subjects.

Explanation

Let P, C and M be the sets of students who have taken physics, chemistry and mathematics respectively.
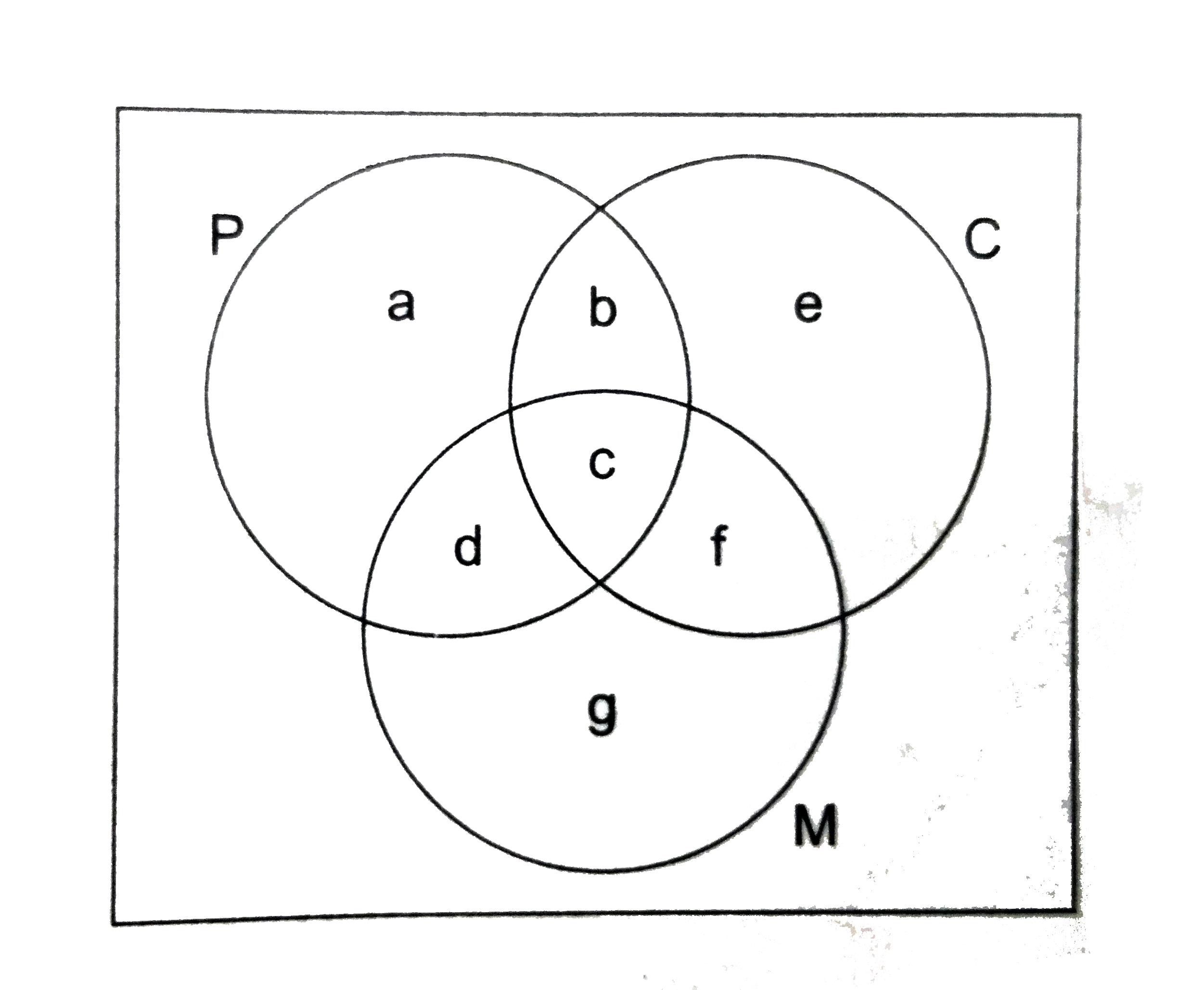
Let a,b,c,d,e,f and g denote the number of students in the respective regions, as shown in the adjoining Venn diagram.
As per data given, we have

From these equations, we get
`c=3,f=2,d=6,b=1`
Now, ` c+d +f+g=15rArr 3+6 +2+g=15 rArr g=4`,
`b+c +e+f=11rArr 1+3+e+2=11rArr e=5`.
`a+b+c+d =12 rArr a+1+3+6=12 rArr a=2`.
`therefore a=2, b=1,c=3,d=6,e=5,f=2 and g=4`.
So, we have :
(i) Number of students who offered physics only `=a=2`.
(ii) Number of stduents who offered chemistry only `=e=5`.
(iii) Number of students who offered mathematics only `g=4`.
(iv) Number of students who offered physics and chemistry but not mathematics `=b=1`.
(v) Number of students who offered physics amd mathematics but not chemistry `=d=6`.
(vi) Number of students who offered only one of the given subjects `=(e+e+g)=(2+5+4)=11`.
(vii) Number of students who offered at least one of the given subjects `=(a + b+c+ d+e +f+ g) =(2+1+3+6+5+2+4)=23`.
(vii) Number of students who offered none of the three given subjects `=(25-23)=2`.