Find the mean, variance and standard deviation of the number of tails in two tosses of a coin.
In two tosses of a coin, the sample space is given by
S={HH,HT,TH,⊤}.
∴ n(S)=4.
So, every single outcome has a probability 14.
Let X= number of tails in two tosses.
In two tosses, we may have no tial. 1 tail or 2 tails.
So, the possible values of X are 0, 1, 2.
P(X=0)=P(getting no tial)=P(HH)=14.
P(X=1)=P(getting 1 tail)=P(HTorTH)=24=12.
P(X=2)=P(getting 2 tails)=P(TT)=14.
Hence, the probability distribution of X is given by

∴ mean ,μ=Σxipi=(0×14)+(1×12)+(2×14)=1.
Variance, σ2=Σx2ipi−μ2
=[(0×14)+(1×12)+(4×14)]−12
=12.
Standard deviation, σ=1√2×√2√2=√22=1.4142=0.707.
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 31
18 Videos
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Objective Questions
30 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B
2 Videos
- PRODUCT OF THREE VECTORSBOOK - RS AGGARWALCHAPTER - PRODUCT OF THREE VECTORSEXERCISE - Objective Questions
34 Videos
Similar Questions
Determine variance and standard deviation of the number of heads in three tosses of a coin.
View SolutionFind the mean, variance and standard deviation of the number heads when three coins are tossed.
View SolutionFind the mean, variance and standard deviation of first n natural numbers.
View SolutionFind the mean and variance of the number of heads in the two tosses of a coin.
View SolutionFind the mean, variance, standard deviation of number 6 in the two throws of a dice.
View SolutionFind the variance and standard deviation for the following data:
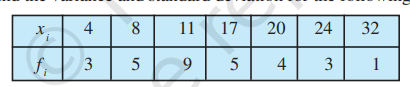
View SolutionFind the variance and standard deviation from the following data:

View SolutionFind the mean, variance and standard deviation using short-cut method
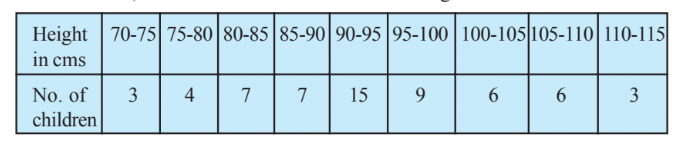
View SolutionFind the mean variance and standard deviation using short-cut method

View SolutionFind the mean, variance and standard deviation using short-cut method.
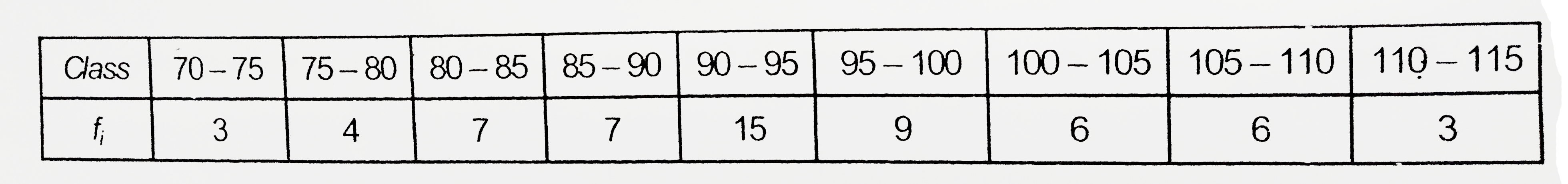
View Solution
