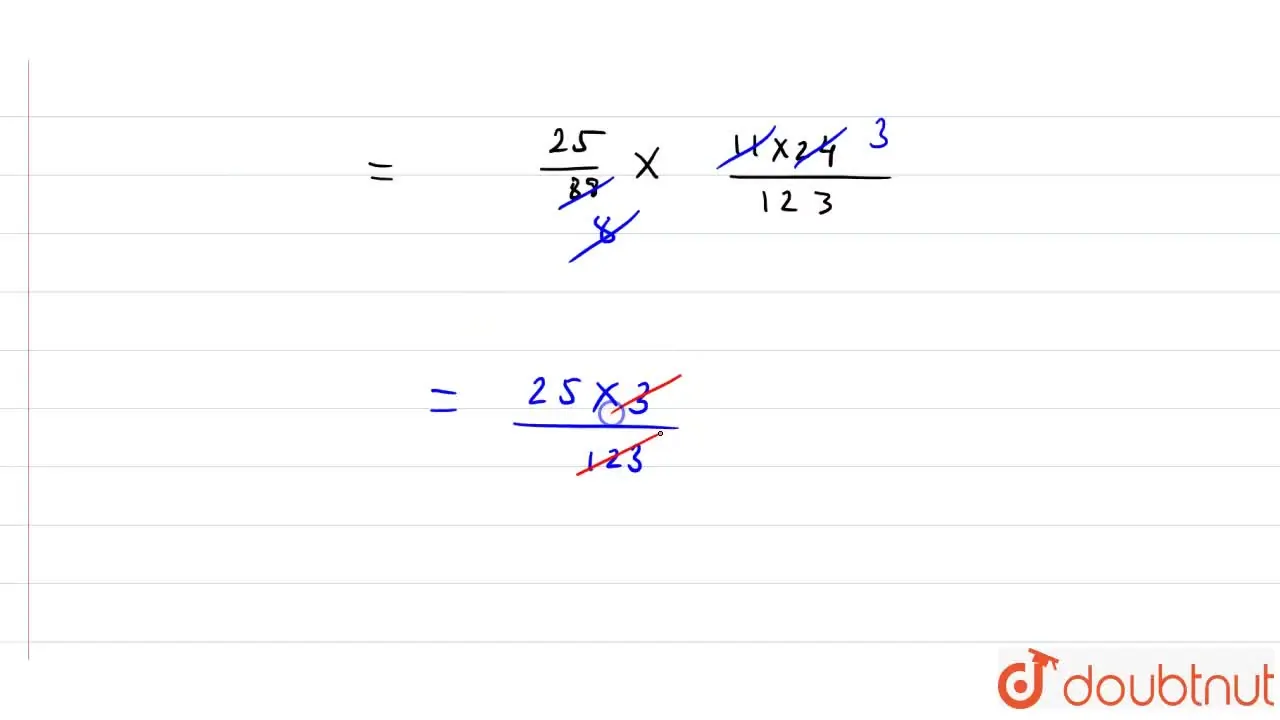There are 5 bags, each containing 5 white balls and 3 black balls. Also, there are 6 bags, each containing 2 white balls and 4 black balls. A white balls is drawn at random. Find the probability that this white ball is from a bag of the first group.
Let = event of selecting a bag from the first group,
= event of selecting a bag from the second group, and
E = event of drawing a white ball.
Then, .
= probability of getting a white ball, given that it is from a bag of the first group
.
= probability of getting a white ball, given that it is from a bag of the second group
Probability of getting the ball from a bag of the first group, given that it is white
[by Bayes's theorem]
.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 3018videos
BAYES'S THEOREM AND ITS APPLICATIONS
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
- BOOK - RS AGGARWALCHAPTER - BINARY OPERATIONSEXERCISE - Exercise 3B8videos
BINARY OPERATIONS
Similar Questions
There are 3 bags, each containing 5 white balls and 3 black balls. Also there are 2 bags, each containing 2 white balls and 4 black balls. A white ball is drawn at random. Find the probability that this white ball is from a bag of the first group.
View SolutionThere are 3 bags, each containing 5 white and 3 black balls. Also, there are 2 bags, each containing 2 white and 4 black balls. A white ball is drawn at random. Find the proqability that this ball is from a bag of the first group.
View SolutionA bag contains 3 white and 5 black balls. One ball is drawn at random. Then, the probability that it is white, is
View SolutionFrom a bag containing 5 white, 3 black and 2 red balls, two balls are drawn at random. Find the probability that both are white.
View SolutionA bag contains 4 white and 5 black balls. A ball is drawn at random from the bag. Find the probability that the ball drawn is white.
View SolutionA bag contains 5 white and 7 red balls. One ball is drawn at random. What is the probability that ball drawn is white?
View SolutionThere are 3 bags each containing 5 white balls and 2 black balls, and 2 bags each containing 1 white ball and 4 black balls, a black ball having been drawn, find the chance that it came from the first group.
View SolutionThere are 3 bags each containing 5 white balls and 2 black balls, and 2 bags each containing 1 white ball and 4 black balls, a black ball having been drawn, find the chance that it came from the first group.
View SolutionA bag contains 4 white, 3 red and 5 black balls. One ball is drawn from the bag. What is the probability that it is white?
View SolutionA bag contains 5 white and 7 red balls. One ball is drawn at random. What is the probability that ball drawn is white?
View Solution