A town has two fire-extinguishing engines, functioning independently. The probability of availability of each engine when needed is 0.95. What is the probability that (i) neither of them is available when needed ? (ii) an engine is available when needed?
The correct Answer is:(i) 1400 (ii) 19200
Let E1= event of availability of the first engine.
And, E2= event of availability of the second engine.
Then, P(E1)=P(E2)=0.95 and P(¯¯¯E1)=P(¯¯¯E2)=(1−0.95)=0.05.
(i) P( neither of them is available when needed)
=P(¯¯¯E1and¯¯¯E2)=P(¯¯¯E1)×P(¯¯¯E2).
(ii) P( an engine is available when needed)
=P[(E1 and not E2)or(E2 and not E1)]
=P[(E1and¯¯¯E2)or(E2and¯¯¯E1)]
=P(E1∩¯¯¯E2)+P(E2∩¯¯¯E1)
={P(E1)×P(¯¯¯E2)}+{P(E2)×P(¯¯¯E1)}.
Topper's Solved these Questions
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B
2 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29A
17 Videos
- METHODS OF INTEGRATION BOOK - RS AGGARWALCHAPTER - METHODS OF INTEGRATION EXERCISE - Objective Questions Ii
56 Videos
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 32
32 Videos
Similar Questions
A scientist has to make a decision on each f the two independent events I and II. Suppose the probability of error in making decision on event I is 0.02 and that on event II is 0.05. Find the probability that he scientist will make the correct decision on (i) both events (ii) only one event
View SolutionA ship is fitted with three engines E1, E2, and E3,. The engines function independently of each other with respective probabilities 12. 14and 14 ,and For the ship to be operational at least two of its engines must function. Let X denote the event that the ship is operational and let X1, X2, and X3 denote respectively the events that the engines E1, E2 and E3,are functioning. Which of the following is (are) true?
View Solution
Knowledge Check
When two dice are rolled, what is the probability that the sum of the numbers appeared on them is 11?
A16B118C19D1A machine operates only when all of its three components function The probabilities of the failures of the first , second and third component are 0.2, 0,3 and 0.5 respectively . What is the probability that the machine will fail ?
A0.70B0.72C0.07Dnone of theseFind out which part of a sentence has an error
A1. Banks were developed to keep people's money safeB2. and to make it availableC3. when they need it.D4. No error
An aircraft has three engines A, B and C. The aircraft crashes if all the three engines fail. The probabilties of failure are 0.03, 0.02 and 0.05 for engines A, B and C respectively. What is probability that the aircraft will not crash ?
View SolutionAn aircraft has three engines A, B and C. The aircraft crashes if all the three engines fail. The probabilities of failure are 0.03, 0.02 and 0.05 for engines A, B and C respectively. What is the probability that the aircraft will not crash?
View SolutionEleven books, consisting of five Engineering books, four Mathematics books and two Physics books, are arranged in a shelf at random. What is the probability that the books of each kind are all together?
View SolutionAn aircraft has three engines A, B and C. The aircraft crashes if all the three engines fail. The probabilties of failure are 0.03, 0.02 and 0.05 for engines A, B and C respectively. What is probability that the aircraft will not crash ?
View SolutionA certain water-supply system consists of a source, three pumping stations, and a destination. Each pump ing station has a probability p (0 < p < 1) of being operable at a specified time to and station functions independently of one another. The stations are connected as shown in figure:
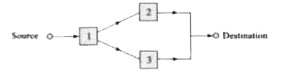
The probability that water is available to the destination at time to is
View Solution
