Question

Find the equation of the perpendicular from point $(3,-1,11)$ to line $\frac{x}{2}=\frac{y-2}{3}=\frac{z-3}{4}$. Also, find the coordinates of foot of perpendicular and the length of perpendicular.

Explanation

The given line is
`(x)/(2)=(y-2)/(3) =(z-3)/(4)=r ` (say) ….(i)

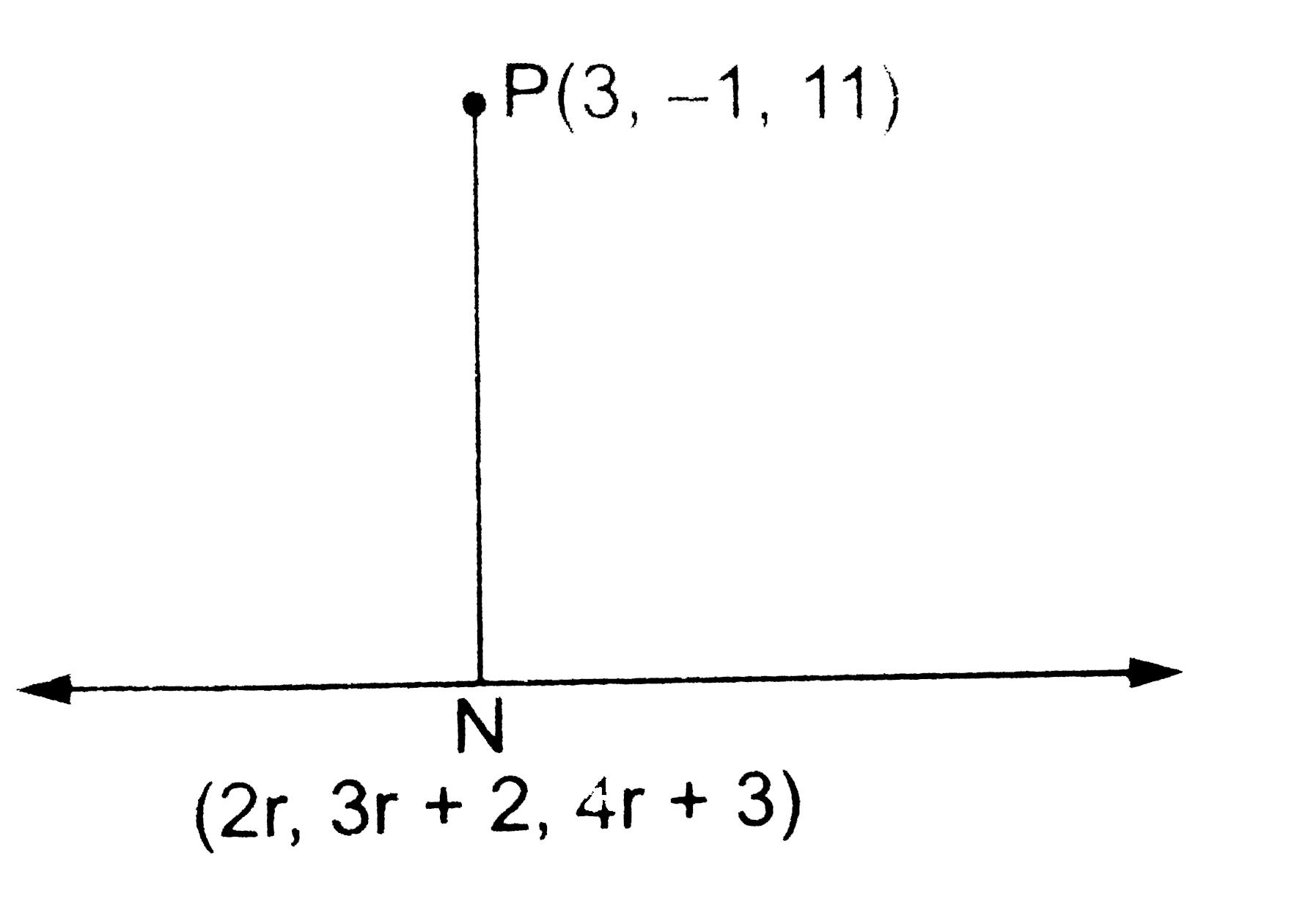
The general point on this line is
`(2r,3r +2, 4r+3)`
Let N be the foot of the perpendicular drawn from the point P(3, -1,11) on
the given line
Then this point is N(2r ,3r +2,4r+3) for some fixed value of r .
D.r.s of PN are (2r -3),(3r+3) (4r-8)
D.r's of the given line (i) are 2,3,4
Since PN is perpendicular to the given line (i) we have
`2(2r-3) +3(3r+3) +4(4r-8) = 0 rArr 29r =29 rArr r=1`
`:. `Dr ' s of PN are -1,6 ,-4 [putting r=1 in (ii) ]
So, the required equations of perpendicular PN are
`(x-3)/(-1) = (y+1)/(6)= (z-11)/(-4)`
Now the coordinates of N are N(2,5,7)[putting r =1]
Length of perpendicular PN
`=sqrt((2-3)^(2) +(5+1)^(2)+(7-11)^(2))=sqrt((-1)^(2)+6^(2)+(-4)^(2))`
`=sqrt(1+36 +16)= sqrt(53)`