Question

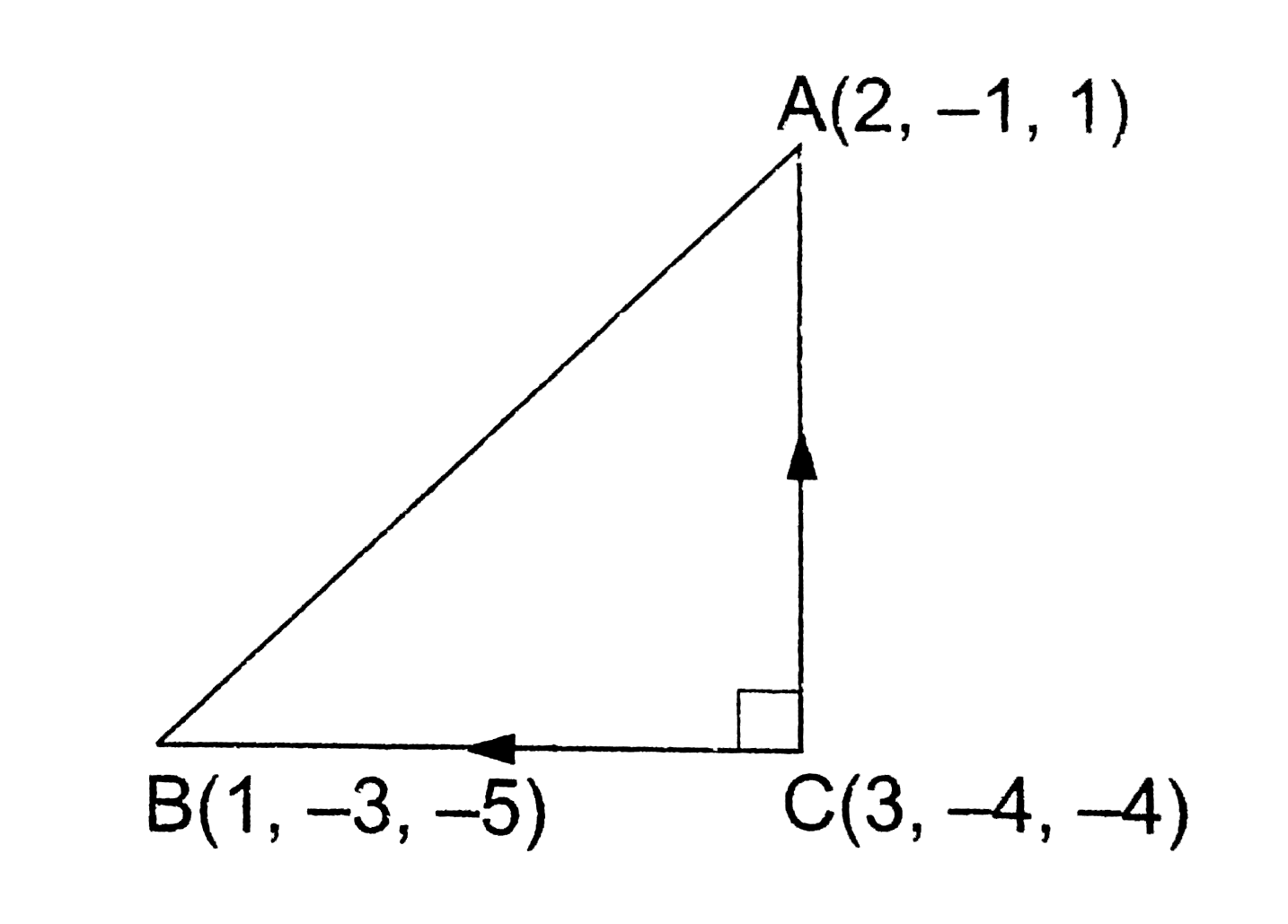
Show that the points, A, B and C having position vectors $(2\hat{i}-\hat{j}+\hat{k}),(\hat{i}-3\hat{j}-5\hat{k})$ and $(3\hat{i}-4\hat{j}-4\hat{k})$ respectively are the vertices of a rightangled triangle. Also, find the remaining angles of the triangle.

Explanation

We have
`vec(AB)=`(p.v. of B)-(p.v. of A)
`=(-hat(i)-2hat(j)-6hat(k))`,
`vec(BC)=` (p.v. of C)-(p.v. of B)
`=)2hat(i)-hat(j)+hat(k))` and
`vec(CA)=` (p.v. of A)-(p.v. of C)`=(-hat(i)+3hat(j)+5hat(k))`.
Clearly, we have `vec(AB)+vec(BC)+vec(CA)=vec(0)`.
`:.` A, B and C are the vertices of a triangle.
Now, `vec(BC).vec(CA)=(2hat(i)-hat(j)+hat(k)).(-hat(i)+3hat(j)+5hat(k))=(-2-3+5)=0`
`:. vec(BC) bot vec(CA)` and therefore, `angleC=90^(@)`.
Now, `angleA` is the angle between `vec(AB)` and `vec(AC)`
`:. vec(AB).vec(AC)=|vec(AB)||vec(AC)| cos A implies cos A = ((vec(AB).vec(AC)))/(|vec(AB)||vec(AC)|)`
=((-hat(i)-2hat(j)-6hat(k)).(hat(i)-3hat(j)-5hat(k)))/({sqrt((-1)^(2)+(-2)^(2)+(-6)^(2))}.{sqrt(1^(2)+(-3)^(2)+(-5)^(2))})`
`[ :' vec(AB)=-vec(CA)]`
`=((-1+6+30))/(sqrt(41)xxsqrt(35))=35/(sqrt(41)xxsqrt(35))=sqrt(35)/sqrt(41)=sqrt(35/41)`
`implies A= cos^(-1) sqrt(35/41)`
Further, `angleB` is the angle between `vec(BC)` and `vec(BA)`
`:. vec(BC).vec(BA)=|vec(BC)||vec(BA)|cos B`
`implies cos B =((vec(BC).vec(BA)))/(|vec(BC)||vec(BA)|)`
`=((2hat(i)-hat(j)+hat(k)).(hat(i)+2hat(j)+6hat(k)))/({sqrt(2^(2)+(-1)^(2)+1^(2))}.{sqrt(1^(2)+2^(2)+6^(2))})`
`=((2-2+6))/(sqrt(6)xxsqrt(41))=6/(sqrt(6)xxsqrt(41))=sqrt(6)/sqrt(41)=sqrt(6/41)`
`implies B= cos^(-1) sqrt(6/41)`
`:. A=cos^(-1) sqrt(35/41), B= cos^(-1) sqrt(6/41)`, and `C=90^(@)`.