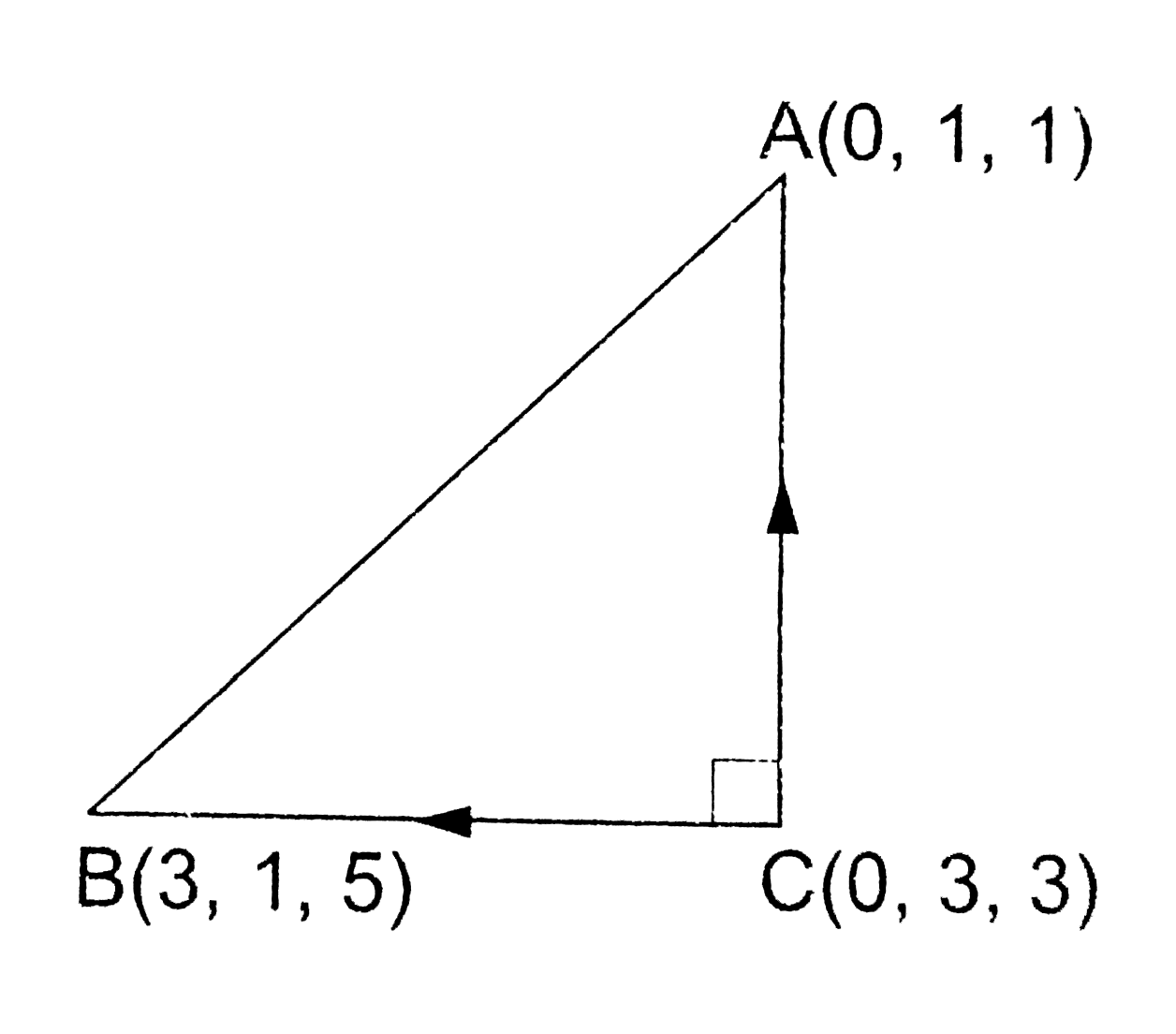
Let $A (0, 1, 1), B (3, 1, 5)$ and $C (0, 3, 3)$ be the vertices of a $△ A B C$ . Using vectors, show that $△ A B C$ is right angled at C.

Video Solution

Text Solution

Verified by Experts

In order to show that $- - \to C A ⊥ - - \to C B$ , we must show that $- - \to C A . - - \to C B = 0$ . Let O be the origin. Then,
$- - \to O A = 0 ˆ i + ˆ j + ˆ k, - - \to O B = 3 ˆ i + ˆ j + 5 ˆ k$ and $- - \to O C = 0 ˆ i + 3 ˆ j + 3 ˆ k$ .
$∴ - - \to C A = (- - \to O A - - - \to O C)$
$= (0 ˆ i + ˆ j + ˆ k) - (0 ˆ i + 3 ˆ j + 3 ˆ k)$
$= (0 - 0) ˆ i + (1 - 3) ˆ j + (1 - 3) ˆ k$
$= (0 ˆ i - 2 ˆ j - 2 ˆ k)$ .
$∴ - - \to C B = (- - \to O B - - - \to O C)$
$= (3 ˆ i + ˆ j + 5 ˆ k) - (0 ˆ i + 3 ˆ j + 3 ˆ k)$
$= (3 ˆ i - 2 ˆ j + 2 ˆ k)$ .
$∴ - - \to C A . - - \to C B = (0 ˆ i - 2 ˆ j - 2 ˆ k) . (3 ˆ i - 2 ˆ j + 2 ˆ k)$
$= [(0 \times 3) + (- 2) \times (- 2) + (- 2) + (- 2) \times 2] = 0$
$\Rightarrow - - \to C A ⊥ - - \to C B$ .
Hence, $Δ A B C$ is right angled at C.

Updated on:21/07/2023

If A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2) are the vertices of $Δ$ ABC, then the triangle is
Ascalane
Bright angled
Cequilateral
Disosceles
Let $A (0, β), B (- 2, 0)$ and $C (1, 1)$ be the vertices of a triangle. Then
Angle A of the triangle ABC will be obtuse if $β$ lies in
A $(- 1, 2)$
B $(2, \frac{5}{2})$
C $(- 1, \frac{2}{3}) \cup (\frac{2}{3}, 2)$
Dnone of these
If A(-1, 2, -3), B(5, 0, -6) and C(0, 4, -1) are the vertices of triangle ABC, then the direction ratios of the internal bisector of $∠ B A C$ are
A(5, 6, 7)
B(4, -3, 9)
C(25, 8, 5)
D(5, 8, 25)