Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes.
Video Solution
Text Solution
The correct Answer is:(x+y)2{1+(dydx)2}=(x+ydydx)2
The equation of the given family of circles is
(x+a)2+(y−a)2=a2…(i), where a is a parameter.
Differentiating (i) w.r.t.x, we get
2(x+a)+2(y−a)dydx=0⇒(x+a)+(y−a)p=0
⇒a=(x+yp)(p−a).
Put this value of a in (i) to get the required equation.
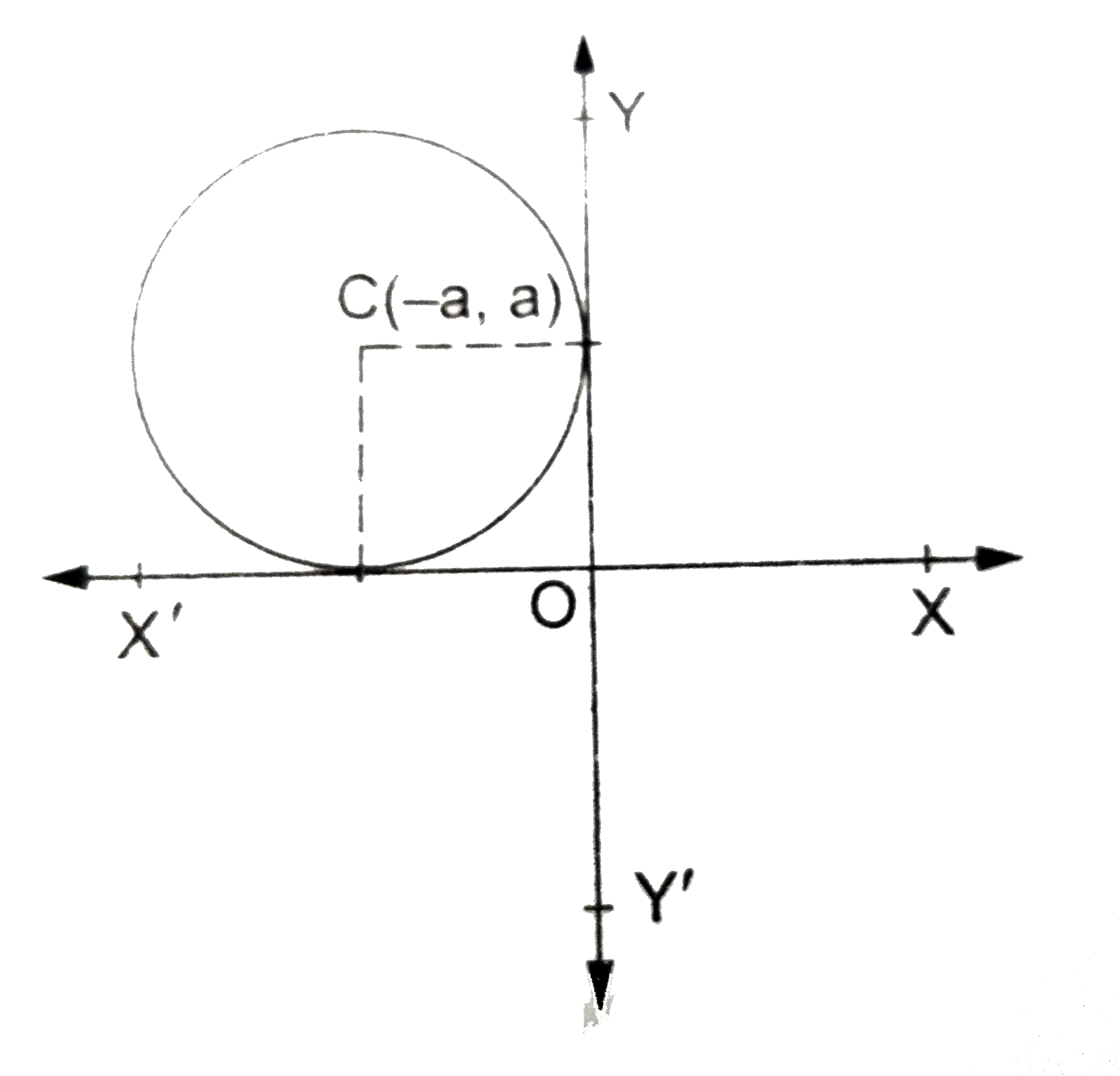
|
Topper's Solved these Questions
- DIFFERENTIAL EQUATIONS AND THEIR FORMATION BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS AND THEIR FORMATION EXERCISE - Exercise 18B
17 Videos
- DETERMINANTSBOOK - RS AGGARWALCHAPTER - DETERMINANTSEXERCISE - Objective Questions
29 Videos
- DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLEBOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLEEXERCISE - Exercise 19B
60 Videos
Similar Questions
Knowledge Check
The differential equation of all circles in the first quadrant which touch the coordiante axes is of order
A1B2C3Dnone of these
Form the differential equation of family of standard circle
View SolutionForm the differential equation of the family of circles touching the y-axis at origin.
View SolutionForm the differential equation of the family of circles touching the x-axis at origin.
View SolutionForm the differential equation of family of circles having center at origin.
View SolutionFind the differential equation of all the circles in the first quadrant which touch the coordinate axes.
View SolutionForm the differential equation of the family of circles having centre on y-axis and radius 3 units.
View SolutionObtain the differential equation of the family of circles :
with centre at (1, 2)
View Solution
