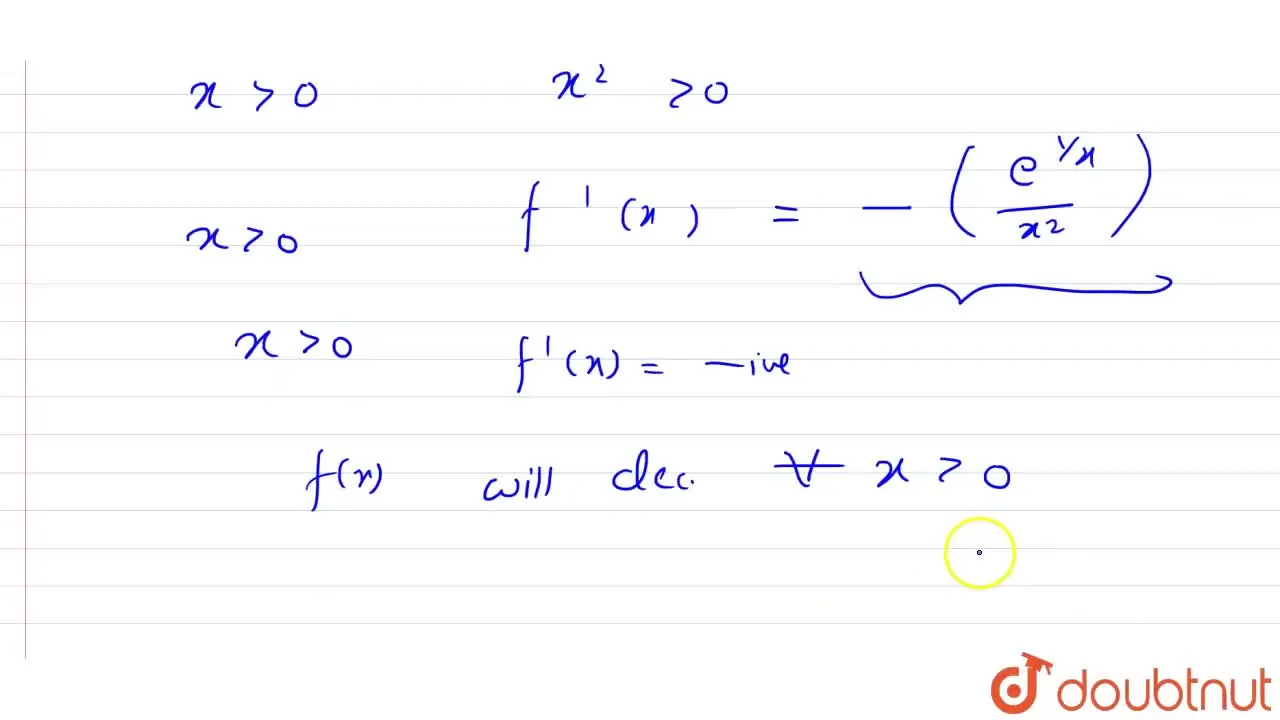Show that f(x)=e1/x is a strictly decreasing function for all x>0
f(x)=e1/x⇒f'(x)=−1x2e1/x<0 for all x>0
[∵x2>0adne1/x>0 when x>0]
Thus, f'(x)<0 for all x>0
Hence, f(x) is strictly decreasing for all x>0
Related Playlists
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11A21videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11B17videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 737videos
ADJOINT AND INVERSE OF A MATRIX
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
Similar Questions
Show that f(x)=e−x is a strictly decreasing function on Rgt
View SolutionShow that f(x)=3x+5 is a strictly increasing function on R
View SolutionProve that f (x) = e3x is strictly increasing function on R.
View SolutionShow that f(x)=e1/x, x≠0 is a decreasing function for all x≠0 .
View SolutionShow that f(x)=e1x,x≠0 is decreasing function for all x≠0.
View SolutionShow that f(x)=(x−1)ex+1 is an increasing function for all x>0 .
View SolutionShow that f(x)=(x−1)ex+1 is an increasing function for all x>0.
View SolutionShow that the function f(x)=ex is strictly increasing on R.
View SolutionShow that the function f(x)=x2 is a strictly decreasing function on (−∞, 0] .
View SolutionShow that the function f(x) = 3 - 2x is strictly decreasing function on R.
View Solution