Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is $\frac{{cos}^{- 1} 1}{\sqrt{3}}$

Video Solution

Text Solution

Verified by Experts

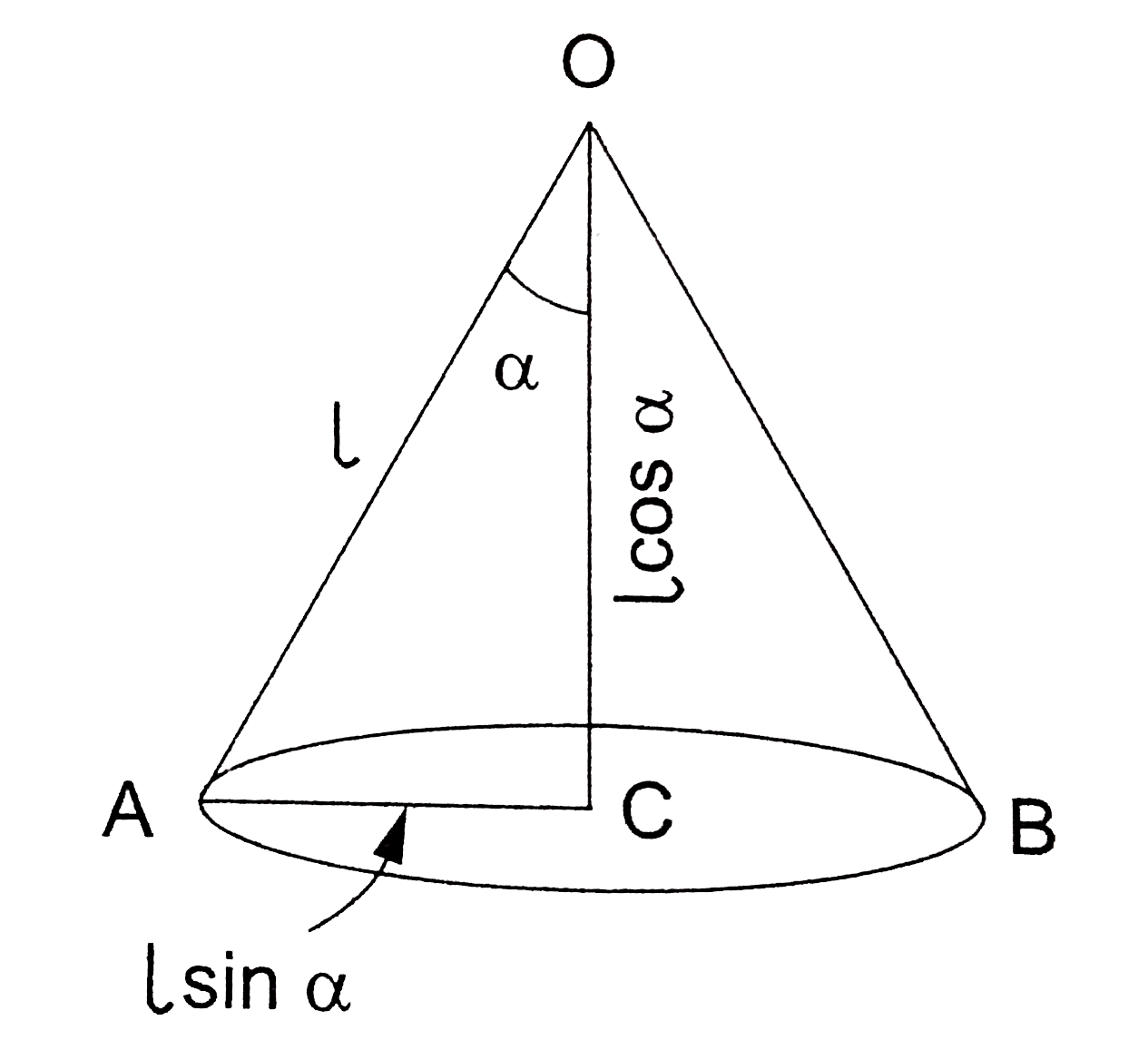
Let $α$ be the semivertical angle of a cone of given slant height l. Then, height of the cone $= l cos α$ , radius of the base $= l sin α$ . Let V be the volume of the cone. Then,
$V = \frac{1}{3} π r^{2} h = \frac{1}{3} π (l^{2} {sin}^{2} α) (l cos α)$
or $V = \frac{1}{3} π l^{3} {sin}^{2} α cos α$
$∴ \frac{d V}{d α} = \frac{1}{3} π l^{3} (- {sin}^{3} α + 2 sin α {cos}^{2} α) = \frac{1}{3} π l^{3} sin α (2 {cos}^{2} α - {sin}^{2} α)$
And, $\frac{d^{2} V}{d α^{2}} = \frac{1}{3} π l^{3} cos α (2 {cos}^{2} α - {sin}^{2} α) + \frac{1}{3} π l^{3} sin α (- 4 sin α cos α - 2 sin α cos α)$
$= \frac{1}{3} π l^{3} {cos}^{3} α (2 - 7 {tan}^{2} α)$
Now, for a maxima or minima, we have $\frac{d V}{d α} = 0$
Now, $\frac{d V}{d α} = 0 \Rightarrow \frac{1}{3} π l^{3} sin α (2 {cos}^{2} α - {sin}^{2} α) = 0$
$\Rightarrow sin α = 0 or 2 {cos}^{2} α - {sin}^{2} α = 0$
$\Rightarrow α = 0 or α = {tan}^{- 1} \sqrt{2}$
Neglecting $α = 0$ , we have $α = {tan}^{- 1} \sqrt{2}$ , i.e., $tan α = \sqrt{2}$
Now, $tan α = \sqrt{2} \Rightarrow {sec}^{2} α = 3 \Rightarrow cos α = \frac{1}{\sqrt{3}} \Rightarrow α = {cos}^{- 1} . \frac{1}{\sqrt{3}}$
$∴ {[\frac{d^{2} V}{d α^{2}}]}_{α = {tan}^{- 1} \sqrt{2}} = \frac{1}{3} π l^{3} . {(\frac{1}{\sqrt{3}})}^{3} (2 - 14) = - \frac{4 π l^{3}}{3 \sqrt{3}} < 0$
Thus, V is maximum when $α = {cos}^{- 1} . \frac{1}{\sqrt{3}}$ , i.e., when the semivertical angle of the cone is ${cos}^{- 1} \frac{1}{\sqrt{3}}$

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

RS AGGARWAL-APPLICATIONS OF DERIVATIVES-Objective Questions

Home
Ask Doubt
Profile