A beam of length l is supported at one end. If W is the uniform load per unit length, the bending moment M at a distance x from the end is given by M=12lx−12Wx2. Find the point on the beam at which the bending moment has the maximum value.
M=(lx2−Wx22)⇒dMdx=(l2−Wx)andd2Mdx2=−W
For a maxima or minima, we have dMdx=0
Now, dMdx=0⇒l2−Wx=0⇒x=l2W
Also, d2Mdx2=−W<0 for all values of x
∴x=l2W is a point of maxima
So, the required point is at a distance of (l/2W) from the supporting end.
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11A
Explore 21 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11B
Explore 17 Videos
- ADJOINT AND INVERSE OF A MATRIXBook:RS AGGARWALChapter:ADJOINT AND INVERSE OF A MATRIXExercise:Exercise 7
Explore 37 Videos
- AREA OF BOUNDED REGIONS Book:RS AGGARWALChapter:AREA OF BOUNDED REGIONS Exercise:Exercise 17
Explore 39 Videos
Similar Questions
A beam of length l is supported at one end. If W is the uniform load per unit length, the bending moment M at a distance x from the end is given by M=12lx−12Wx2. Find the point on the beam at which the bending moment has the maximum value.
View SolutionA beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2x−W2x2 . Find the point at which M is maximum.
View Solution
Knowledge Check
A string of length L and mass M hangs freely from a fixed point. Then the velocity of transverse waves along the string at a distance x from the free end is
A√gLB√gxCgLDgx
A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=Wx3−W3x3L2 . Find the point at which M is maximum.
View SolutionA beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by M=WL2×−W2x2 Find the point at which M is maximum in each case.
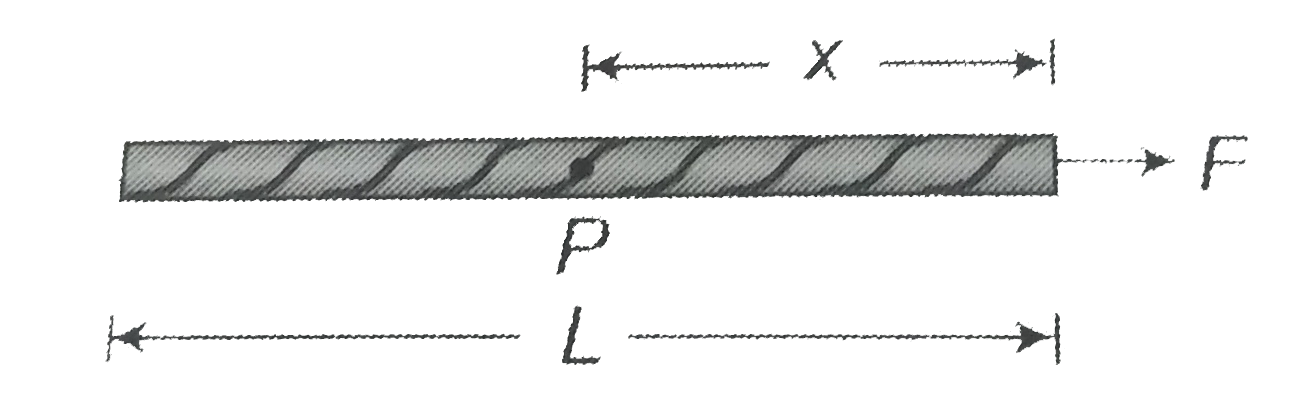
View SolutionA uniform rope of length of length L is pulled by a force F on a smooth surface. Find tension in the rope at a distance x from the end where force is applied.
View SolutionThe radius of gyration of a uniform rod of mass m and length l about an axis perpendicular to its length and at distance l4 from its one end will be
View SolutionA uniform rope of mass M and length L, on which a force F is applied at one end, then find stress in the ropw at a distance x form the end where force is applied?
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionA uniform thin rod of length 3L is bent at right angles at a distance L from one end as shown in Fig. If length of rod is 1.8m, find the co-ordinates and position vector of the mass of the system.

View Solution