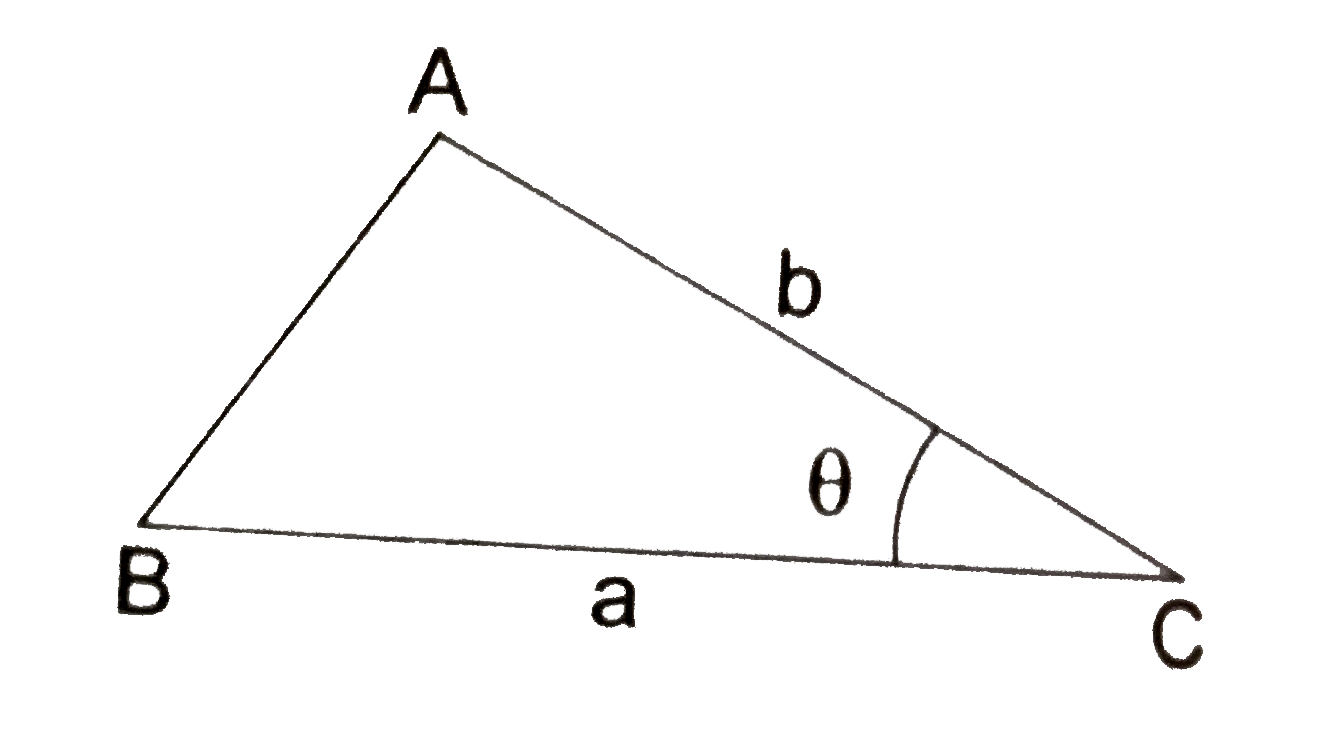
Two sides of a triangle are given. The angle between them such that the area is maximum, is given by

Video Solution

Text Solution

Verified by Experts

Let a and b be the lengths of the given sides and let $θ$ be the angle between them. Let A be the area of the triangle
Then, $A = \frac{1}{2} a b sin θ$
$∴ \frac{d A}{d t h η} = \frac{1}{2} a b cos θ and \frac{d^{2} A}{d θ^{2}} = - \frac{1}{2} a b sin θ$
Now, $\frac{d A}{d θ} = 0 \Rightarrow \frac{1}{2} a b cos θ = 0 \Rightarrow cos θ = 0 \Rightarrow θ = \frac{π}{2}$
And, ${[\frac{d^{2} A}{d θ^{2}}]}_{θ = (π / 2)} = - \frac{1}{2} a b sin \frac{π}{2} = - \frac{1}{2} a b < 0$
$∴ θ = \frac{π}{2}$ is a point of maximum.
Hence, the area of the triangle is maximum when the angle between the given sides is $(π / 2)$

Updated on:21/07/2023

If PQ and PR the two sides of a triangle, then the angle between them which gives maximum area of the triangle is
A $\frac{π}{2}$
B $\frac{π}{3}$
C $\frac{π}{4}$
D $π$
Two sides of a triangle are 6 m and 8 m long , and angle between them is increasing at the rate of $2^{\circ}$ per sec. When the angle between them is $60^{\circ}$ , the third side is increasing at the rate of
A $\frac{2 π}{5 \sqrt{39}} m / s$
B $\frac{5 π}{2 \sqrt{39}} m / s$
C $\frac{2 \sqrt{39}}{5 π} m / s$
D $\frac{10 π}{\sqrt{39}} m / s$
If two sides of a triangle are each k, then its maximum area is
A $k^{2}$
B $\frac{k^{2}}{2}$
C $2 k^{2}$
D $\frac{\sqrt{3} k^{2}}{4}$