A man 160 cm tall, walks away from a source of light situated at the top of a pole 6m high at the rate of 1.1 m/sec. How fast is the length of his shadow increasing when he is 1 metre away from the pole.

Video Solution

Text Solution

Verified by Experts

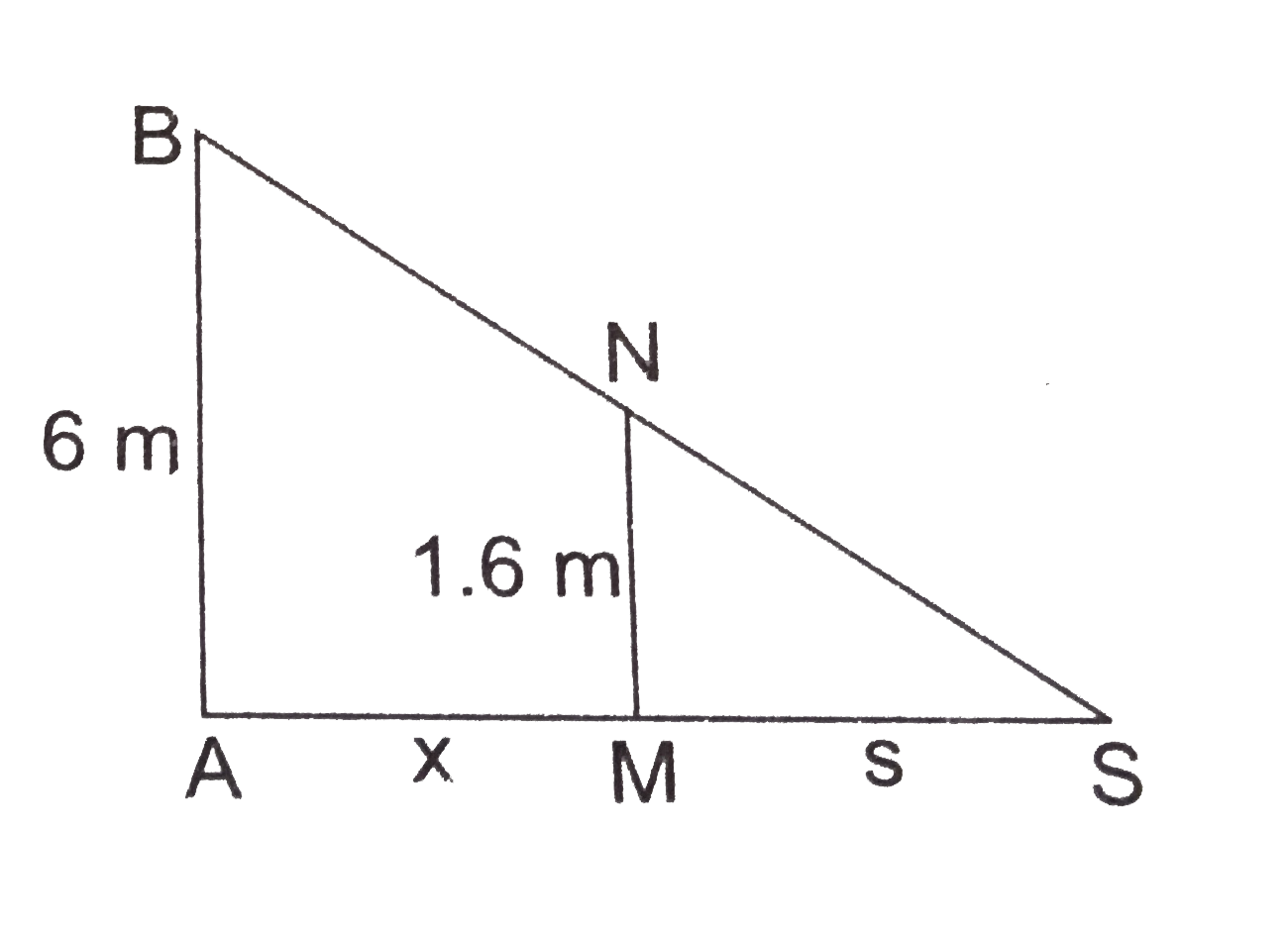
Let AB be the lamp post, the lamp being at B.
Then, AB = 6m.
At an y instance t, let MN be the position of the man nad MS be his shadow. Then MN = 1.6 m
Let AM = x metres and MS = s metres
Given that $\frac{d x}{d t} = 1.1 m / s$ .
Clearly, $△ S A B ~ △ S M N$
$∴ \frac{A S}{M S} = \frac{A B}{M N} = \frac{6}{1.6} = \frac{15}{4}$
$\Rightarrow \frac{x + s}{s} = \frac{15}{4} \Rightarrow x = \frac{11}{4} s$ , where MS = s
$\Rightarrow \frac{d x}{d t} = \frac{11}{4} . \frac{d s}{d t} \Rightarrow 1.1 = \frac{11}{4} . \frac{d s}{d t}$
$\Rightarrow \frac{d s}{d t} = (\frac{1.1 \times 4}{11}) = 0.4 m / s$
Hence, the length of the shadow is increasing at the rate of 0.4 m/s

Updated on:21/07/2023