The two equal sides of an isosceles triangle with fixed base $b$ are decreasing at the rate of $3 c m / s .$ How fast is the area decreasing when the two equal sides are equal to the base?

Video Solution

Text Solution

Verified by Experts

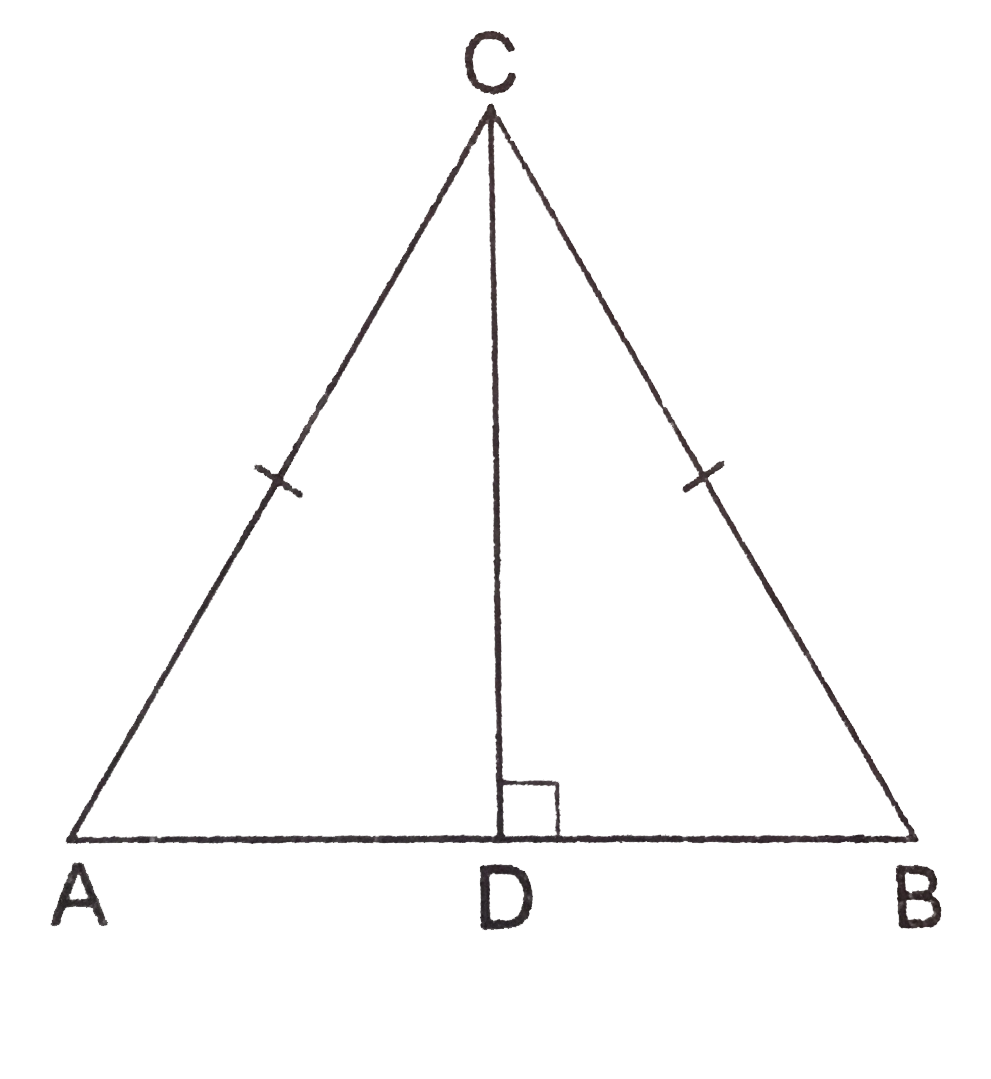
At a certain instant t, let $△ A B C$ be an isosceles triangle in which AB = AC = x cm and BC = b cm
Then, $\frac{d x}{d t} = 3 c m / sec$ (given)...(i)
Draw $A D ⊥ B C$ . Then, $B D = D C = \frac{b}{2}$
$∴ A D = \sqrt{x^{2} - \frac{b^{2}}{4}} = \frac{\sqrt{4 x^{2} - b^{2}}}{2}$
$∴ A = \frac{1}{2} b . \frac{\sqrt{4 x^{2} - b^{2}}}{2} = \frac{b \sqrt{4 x^{2} - b^{2}}}{4}$
$\Rightarrow \frac{d A}{d t} = \frac{d A}{d x} . \frac{d x}{d t}$
$= (\frac{d A}{d x} \times 3) [∵ \frac{d x}{d t} = 3 c m / sec]$
$= \frac{d}{d x} {\frac{b \sqrt{4 x^{2} - b^{2}}}{4}} \times 3$
$= \frac{3 b}{4} . \frac{1}{2} {(4 x^{2} - b^{2})}^{- 1 / 2} . (8 x) = \frac{3 b x}{\sqrt{4 x^{2} - b^{2}}}$
$∴ {[\frac{d A}{d t}]}_{x = b} = \frac{3 b^{2}}{\sqrt{4 b^{2} - b^{2}}} = \frac{3 b^{2}}{\sqrt{3} b} = \sqrt{3} b$

Updated on:21/07/2023

Each of the two equal sides of an isosceles right triangle is 10 cm long. Its area is
A $5 \sqrt{10} c m^{2}$
B50 $c m^{2}$
C $10 \sqrt{3} c m^{2}$
D75 $c m^{2}$
Each of equal sides of an isosceles triangle is 13 cm. If the length of base is 24 cm then its area is
A $50 c m^{2}$
B $60 c m^{2}$
C $55 c m^{2}$
D $65 c m^{2}$
Each of the equal sides of an isosceles triangle is 13 cm and its base is 24 cm. The area of the triangle is
A156 $c m^{2}$
B78 $c m^{2}$
C60 $c m^{2}$
D120 $c m^{2}$