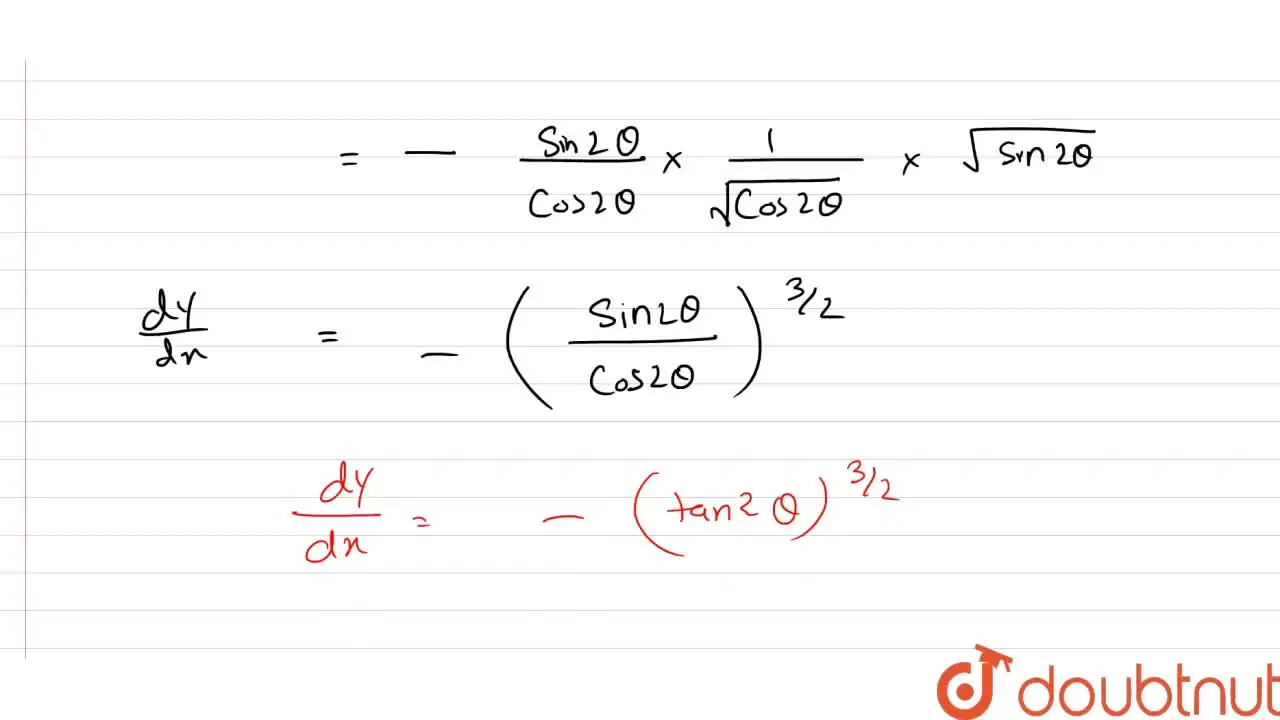
Find dydx, when
x=√sin2θ,y=√cos2θ
Video Solution
Text Solution
The correct Answer is:−(tan2θ)
|
Answer
Step by step video, text & image solution for Find (dy)/(dx), when x=sqrt(sin 2theta), y=sqrt(cos 2theta) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIATIONEXERCISE - Exercise 10H10videos
DIFFERENTIATION
- BOOK - RS AGGARWALCHAPTER - DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLEEXERCISE - Exercise 19B60videos
DIFFERENTIAL EQUATIONS WITH VARIABLE SEPARABLE
- BOOK - RS AGGARWALCHAPTER - FUNCTIONSEXERCISE - Exercise 2D11videos
FUNCTIONS
Similar Questions
Find dydx , when x=a(θ+sinθ) and y=a(1−cosθ)
View SolutionFind dydx, when x=a(θ+sinθ)andy=a(1−cosθ)
View SolutionFind dydx , when x=a(1−cosθ) and y=a(θ+sinθ) at θ=π2
View SolutionFind dydx, when x=aeθ(sinθ−cosθ),y=aeθ(sinθ+cosθ)
View SolutionFind dydx , when x=aeθ(sinθ−cosθ), y=aeθ(sinθ+cosθ)
View SolutionFind dydx , when x=b sin2θ and y=a cos2θ
View SolutionFind dydx, when
x=cosθ+cos2θ,y=sinθ+sin2θView SolutionFind dydx , when x=acosθ and y=bsinθ
View SolutionFind dydx if x=a(θ−sinθ) and y=a(1−cosθ)
View SolutionFind dydxifx=a(θ−sinθ)andy=a(1−cosθ).
View Solution