If PQRS are four different ligands, then how many geometric isomers will be found for square planar [Pt.PQRS]2+ ?
The correct Answer is:3
To determine the number of geometric isomers for the complex (Pt(PQRS))2+ where PQRS are four different ligands, we can follow these steps:
Step 1: Understand the Geometry
The complex is square planar, which means that the ligands will be arranged in a two-dimensional plane around the central platinum ion.
Step 2: Fix One Ligand
To simplify the counting of isomers, we can fix one ligand in a position. Let's fix ligand P at one position.
Step 3: Position the Remaining Ligands
With P fixed, we need to arrange the remaining three ligands (Q, R, and S) in the remaining three positions. The arrangement of these ligands will determine the geometric isomers.
Step 4: Identify Possible Arrangements
1. First Arrangement: Place Q opposite P. The remaining two ligands R and S can be arranged in the other two positions. This gives us one geometric isomer:
- P, Q, R, S (with Q opposite P)
2. Second Arrangement: Place R opposite P. The remaining two ligands Q and S can be arranged in the other two positions. This gives us a second geometric isomer:
- P, R, Q, S (with R opposite P)
3. Third Arrangement: Place S opposite P. The remaining two ligands Q and R can be arranged in the other two positions. This gives us a third geometric isomer:
- P, S, Q, R (with S opposite P)
Step 5: Count the Isomers
From the arrangements above, we can see that there are three distinct geometric isomers possible when P is fixed and the opposite ligand is varied among Q, R, and S.
Conclusion
Thus, the total number of geometric isomers for the complex (Pt(PQRS))2+ is 3.
The complex is square planar, which means that the ligands will be arranged in a two-dimensional plane around the central platinum ion.
To simplify the counting of isomers, we can fix one ligand in a position. Let's fix ligand P at one position.
With P fixed, we need to arrange the remaining three ligands (Q, R, and S) in the remaining three positions. The arrangement of these ligands will determine the geometric isomers.
1. First Arrangement: Place Q opposite P. The remaining two ligands R and S can be arranged in the other two positions. This gives us one geometric isomer:
- P, Q, R, S (with Q opposite P)
2. Second Arrangement: Place R opposite P. The remaining two ligands Q and S can be arranged in the other two positions. This gives us a second geometric isomer:
- P, R, Q, S (with R opposite P)
- P, S, Q, R (with S opposite P)
From the arrangements above, we can see that there are three distinct geometric isomers possible when P is fixed and the opposite ligand is varied among Q, R, and S.
Thus, the total number of geometric isomers for the complex (Pt(PQRS))2+ is 3.
Topper's Solved these Questions
- CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 24- HALOALKANES AND HALOARENES
15 Videos
- CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 25- ALCOHOLS, PHENOLS AND ETHER
15 Videos
- CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC/INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 22- THE D- AND F-BLOCK ELEMENTS
15 Videos
- BIOMOLECULES BOOK - DISHA PUBLICATIONCHAPTER - BIOMOLECULES EXERCISE - Exercise - 2 : Concept Applicator
30 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTURE BOOK - DISHA PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTURE EXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
Similar Questions
Knowledge Check
How many geometrical isomers are possible for
 A2B3C4D8
A2B3C4D8How many geometrical isomers of this compound are possible ?
 A0B2C3D4
A0B2C3D4How many geometrical isomers of this compound are possible:
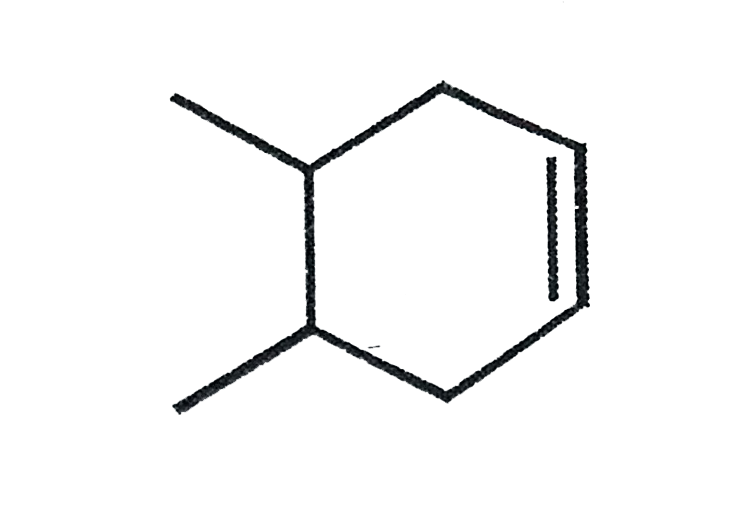 A0B2C3D4
A0B2C3D4
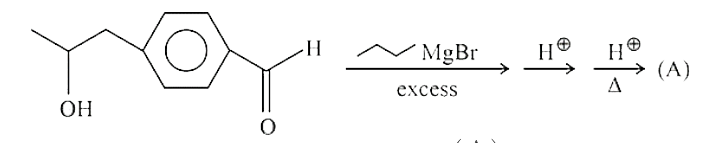
How many geometrical isomer of (A) is possible?
View Solution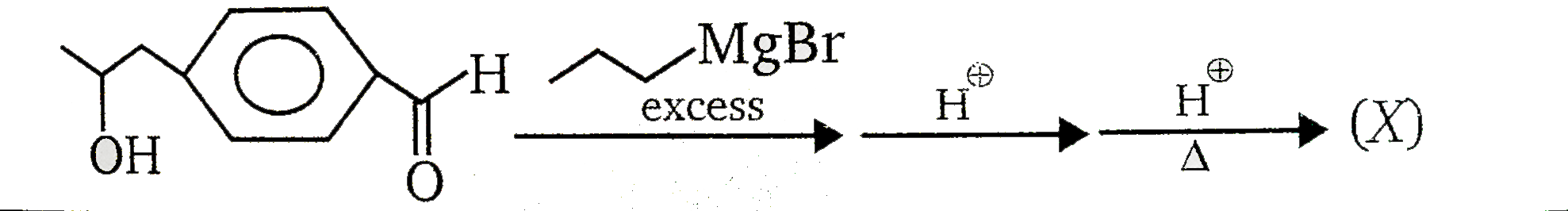
How many geometrical isomer of (X) is possible ?
View Solution
How many geometrical isomers are possible for the above compound ?
View Solution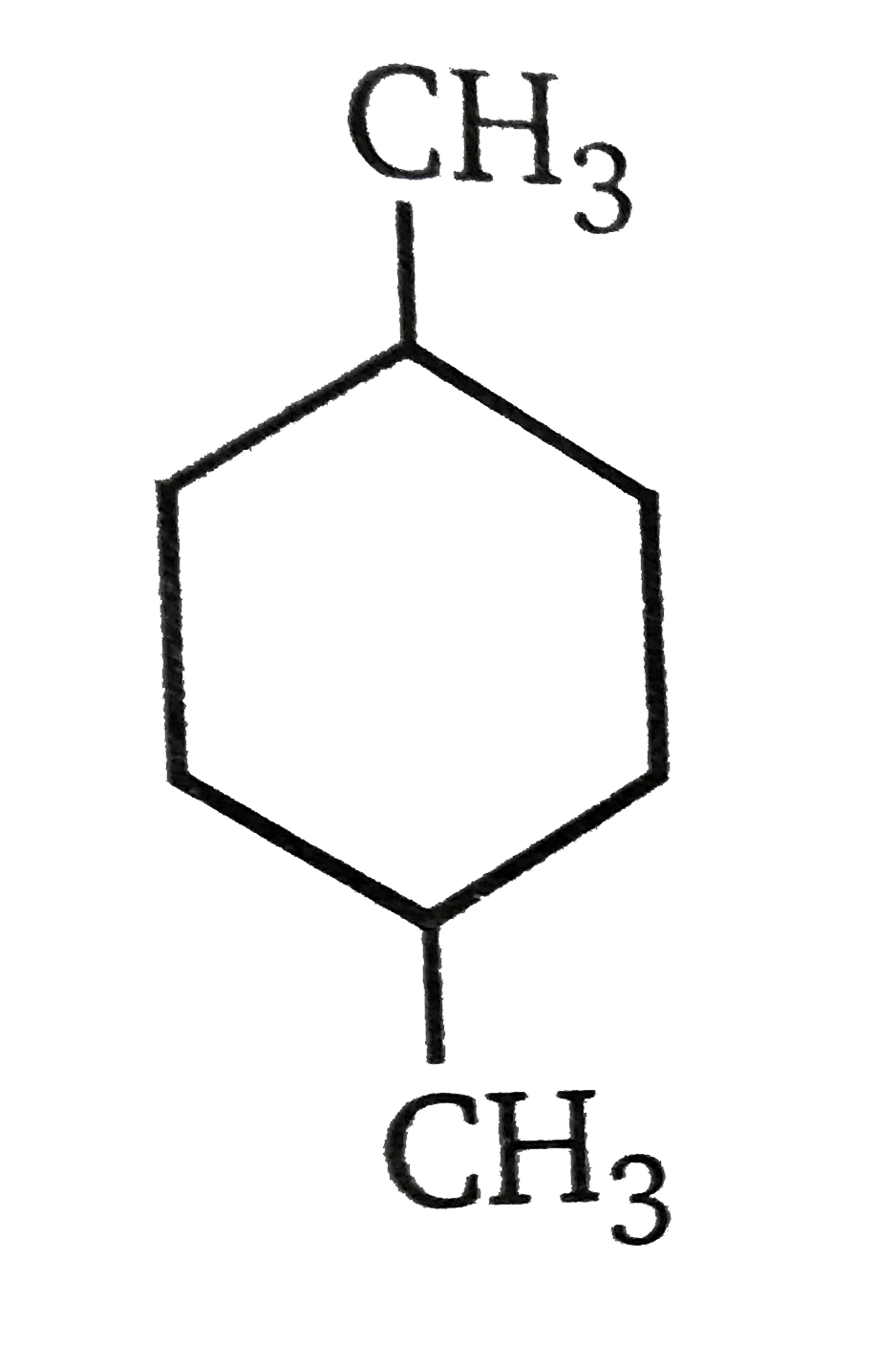
How many geometrical isomers are possible for the above compound ?
View Solution
How many geometrical isomers are possible for the above compound ?
View Solution


