Pipe A has length twice the pipe B. Pipe A has both ends open and pipe B has one end open. Which harmonics of pipe A have a frequency that matches a resonance frequency of pipe B.
To solve the problem, we need to determine which harmonics of pipe A (which is open at both ends) resonate at the same frequency as the harmonics of pipe B (which is open at one end and closed at the other).
1. Define Lengths of Pipes:
- Let the length of pipe B be L.
- Therefore, the length of pipe A will be 2L (since pipe A is twice the length of pipe B).
2. Determine Wavelengths:
- For pipe B (open at one end and closed at the other), the fundamental frequency has a wavelength given by:
λB=4L
- For pipe A (open at both ends), the wavelength for the fundamental frequency is:
λA=2L
3. Calculate Frequencies:
- The frequency of sound in a pipe is given by the formula:
f=vλ
- For pipe B, the frequency can be expressed as:
fB=vλB=v4L
- The harmonics of pipe B can be expressed as:
f_B = \frac{(2n - 1)v}{4L} \quad \text{(where n = 1, 2, 3, \ldots )}
- For pipe A, the frequency is:
fA=vλA=v2L
- The harmonics of pipe A can be expressed as:
f_A = \frac{m v}{2L} \quad \text{(where m = 1, 2, 3, \ldots )}
4. Set Frequencies Equal:
- To find the harmonics that match, we set fA equal to fB:
(2n−1)v4L=mv2L
- Cancel v and L from both sides:
2n−1=2m
5. Solve for Harmonics:
- Rearranging gives:
2n=2m+1⇒n=m+12
- Since n must be an integer, m must be an integer such that m is odd. Thus, m can take values like 1, 3, 5, etc.
6. Conclusion:
- The harmonics of pipe A that match the resonance frequencies of pipe B are those where m is odd (1, 3, 5, ...), corresponding to n values of 1, 2, 3, ... respectively.
Final Answer:
The harmonics of pipe A that match the resonance frequencies of pipe B are the odd harmonics of pipe A.
- Let the length of pipe B be L.
- Therefore, the length of pipe A will be 2L (since pipe A is twice the length of pipe B).
- For pipe B (open at one end and closed at the other), the fundamental frequency has a wavelength given by:
λB=4L
- For pipe A (open at both ends), the wavelength for the fundamental frequency is:
λA=2L
- The frequency of sound in a pipe is given by the formula:
f=vλ
- For pipe B, the frequency can be expressed as:
fB=vλB=v4L
- The harmonics of pipe B can be expressed as:
f_B = \frac{(2n - 1)v}{4L} \quad \text{(where n = 1, 2, 3, \ldots )}
- For pipe A, the frequency is:
fA=vλA=v2L
- The harmonics of pipe A can be expressed as:
f_A = \frac{m v}{2L} \quad \text{(where m = 1, 2, 3, \ldots )}
- To find the harmonics that match, we set fA equal to fB:
(2n−1)v4L=mv2L
- Cancel v and L from both sides:
2n−1=2m
- Rearranging gives:
2n=2m+1⇒n=m+12
- Since n must be an integer, m must be an integer such that m is odd. Thus, m can take values like 1, 3, 5, etc.
- The harmonics of pipe A that match the resonance frequencies of pipe B are those where m is odd (1, 3, 5, ...), corresponding to n values of 1, 2, 3, ... respectively.
The harmonics of pipe A that match the resonance frequencies of pipe B are the odd harmonics of pipe A.
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 15 : (ELECTRIC CHARGES AND FIELDS)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 16 : (ELECTROSTATIC POTENTIAL AND CAPACITANCE)
11 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 13: (OSCILLATIONS)
15 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
Pipe A , with length L , and pipe B , with length 2l , both have two open ends. Which harmonic of pipe B has the same frequency as the fundamental of pipe A ?
View SolutionThe two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second towards resonant freiquency of that pipe. Sound from pipe A set up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B in meter is :

View Solution
Knowledge Check
Two pipes are submerged in sea water , arranged as shown in figure . Pipe (A) with length LA=1.5m and one open end , contains a small source that sets up the standing wave with the second lowest resonant frequency of that pipe . Sound from pipe A sets up resonance in pipe B , which has both ends open . The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B is :
 A1mB1.5mC2mD3m
A1mB1.5mC2mD3m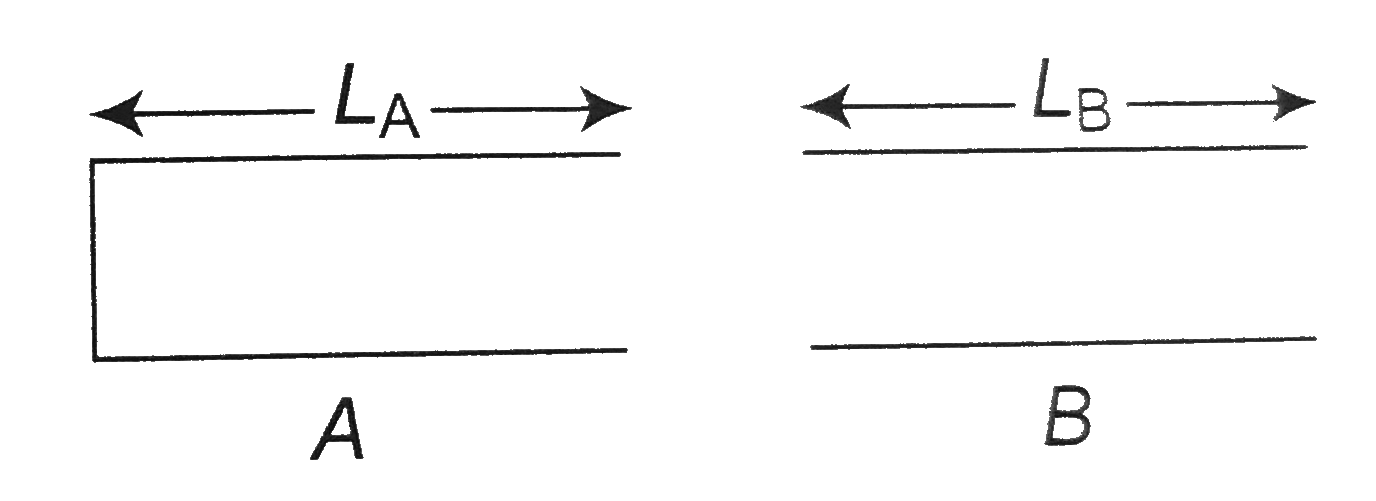
The two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second lowest resonant frequency of that pipe. Sound from pipe A sets up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B isA1mB1.5 mC2 mD3 mA pipe open at both ends gives frequencies which are
Aonly even multiples of fundamental frequency.Bonly odd multiples of fundamental frequency.Call integral multiples of fundamental frequency.Dall fractional multiple of fundamental frequency.
Organ pipe A, with both ends open, has a fundamental frequency of 425 Hz. The fifth harmonic of organ pipe B, with one end open, has the same frequency as the second harmonic of pipe A. How long are (a) pipe A and (b) pipe B?
View Solution
The two pipes are submerged in sea water, arranged as shown in figure. Pipe A with length LA=1.5m and one open end, contains a small sound source that sets up the standing wave with the second lowest resonant frequency of that pipe. Sound from pipe A sets up resonance in pipe B, which has both ends open. The resonance is at the second lowest resonant frequency of pipe B. The length of the pipe B is
View SolutionThe harmonics which are present in a pipe open at one end are
View SolutionPipe A is 0.50 m long and open at both ends. Pipe B is open at one end and closed at the other end. Determine the length of pipe B so that it has the same fundamental frequency as A.
View SolutionIn open organ pipe, first overtone produced is of such frequency that length of the pipe is equal to
View Solution
