A particle which is experiencing a force given by $\to F = 3 \to i - 12 \to j$ , undergoes a displacement of $\to d = 4 \to i$ . If the particle had a kinetic energy of 3 J at the beginning of the displacement, what is its kinetic energy (in joule) at the end of the displacement?

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we will follow these steps:
Step 1: Identify the Given Information
We have:
- Force $\to F = 3^i - 12^j$ N
- Displacement $\to d = 4^i$ m
- Initial kinetic energy $K E_{i} = 3$ J
Step 2: Calculate the Work Done
The work done $W$ by the force during the displacement can be calculated using the dot product of the force and displacement vectors:
$W = \to F \cdot \to d$
Calculating the dot product:
$\to F \cdot \to d = (3^i - 12^j) \cdot (4^i) = 3 \cdot 4 + (- 12) \cdot 0 = 12 + 0 = 12 J$
Step 3: Apply the Work-Energy Theorem
According to the work-energy theorem, the change in kinetic energy is equal to the work done:
$K E_{f} - K E_{i} = W$
Where:
- $K E_{f}$ is the final kinetic energy.
- $K E_{i}$ is the initial kinetic energy.
Rearranging the equation gives us:
$K E_{f} = W + K E_{i}$
Step 4: Substitute the Values
Now we can substitute the values we have:
$K E_{f} = 12 J + 3 J = 15 J$
Final Answer
The final kinetic energy of the particle at the end of the displacement is $15$ J.
---

Updated on:7/8/2024

A particle is executing SHM with an amplitude 4 cm. the displacment at which its energy is half kinetic and half potential is
A1 cm
B $2^{1 / 2} c m$
C $2 c m$
D $2 {(2)}^{1 / 2} c m$
For a particle performing a S.H.M. the potential and kinetic energies will be equal when the displacement of the particle is
AA
B $\frac{A}{2}$
C $A \sqrt{2}$
D $\frac{A}{\sqrt{2}}$
A particle is acted upon by a force F which varies with position x as shown in figure. If the particle at x * 0 has kinetic energy of 25 J, then the kinetic energy of the particle at x = 16 m is

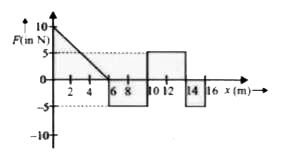A45 J
B30 J
C70J
D20 J